Так там вроде бы всё больше нуля.
Или это я так понял?
Стандартное понимание такое: для

предполагается
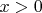
,

--- произвольное действительное. По крайней мере, нас так в школе учили.
Есть ещё другое возведение в степень:

--- произвольное ненулевое целое,

--- произвольное целое либо

и

--- положительное целое.
На пересечении своих областей определения эти два возведения в степень совпадают.
А автор темы, насколько я понял, требует лишь, чтобы

было больше нуля, а

и

у него произвольные.
...для всех вещественных

Продифференцируем это тождество сначала по

...
Вроде в условии не то что дифференцируемость, а даже непрерывность не требуется!