alekcey писал(а):
То, что Вы называете системой уравнений, в данной постановке ею не является. Здесь и неравенства и равенства.
Я полностью согласен, что неправильно назвал эту систему, просто я не знаю, как ее назвать. Реально эта система уравнений-и-неравенств сводится к обычной системе нелинейных уравнений, если заранее знать, какие

и, соответственно
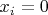
. Но, к сожалению, заранее это неизвестно.
alekcey писал(а):
Надо показывать задачу…
Не совсем понял. Показать вид функций

в явном виде? Это не так просто - задача не единичная. Реально эти функции имеют вид

, где

и

являются функциями от
