Давайте пошагово рассмотрим на примере вашей формулы:
(1) Имеем

(2) Формула приводится к н. ф. "снизу-вверх", то есть начиная с самых глубоких подформул, вы так и сделали. Имеем

, переменную можно не переименовывать, так как

всё одно не входит свободно в

:

.
(3) Теперь из левого конъюнкта выносим

, во второй конъюнкт

вободно не входит, поэтому можно не переименовывать:

.
(4) Выносим из первого конъюнкта

:

.
(5) Теперь из второго конъюнкта выносим

, так как

теперь входит свободно в первый конъюнкт, то

переименуем в

:

.
(6) Далее выносим
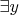
, по аналогичным причинам переименовываем:

.
Кто-то быть может скажет, что один квантор можно было сэкономить, но это не принципиально.