здравствуйте. помогите пожалуйста решить примерчик


е в степени -х в квадрате

 струна бесконечная
струна бесконечнаядошла до состояния:

Это ответ или можно что-то сделать?
и еще один

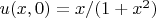

sin

 струна бесконечная
струна бесконечнаядошла до состояния:

sin

sin

Что делать с дробью не представляю...попыткапривести к общему знаменателю провалилась

запись только длиннее получается
заранее спасибо
lilit, вот как надо делать:Степень: e^x, но e^{...} (сложное выражение заключаем в фигурные скобки: e^{-x^2} ---

).
Индекс: U_t и U_{...}, U_{tt} даёт

.
\sin x (пробел после имени функции, палочка \ перед ним).
Дробь: \dfrac{верх}{низ}.