Ну вроде всё не так сложно оказалось

Для каждого неотрицательного действительного

пусть

и

.
Лемма 1. Пусть

--- непрерывное отображение, такое что

. Тогда

и

не может быть продолжено до непрерывного отображения

в

.
Доказательство. Доказываем индукцией по

. Для

всё очевидно. Считаем, что

и для

то, что нужно, уже доказано.
Под экватором понимаем произвольное сечение

проходящей через ноль гиперплоскостью, полюс --- наиболее удалённая от экватора точка

.
Предположим, что некоторое

не попадает в образ

. Пусть

--- экватор с полюсом

. В силу выбора

на

определена функция

, которая для каждого

равна точке пересечения экватора

с полуплоскостью, проходящей через соединяющую полюса прямую и

. Легко видеть, что

есть отображени

в

с требуемым свойством. Заменяя при необходимости

на

, будем считать, что

.
Пусть теперь

равно пересечению

с гиперплоскостью, содержащей

. Для каждой точки

пусть

равно элементу

, ортогональная проекция которого на

равна

и который лежит по ту же сторону от

, что и

. Тогда

есть непрерывное отображение

в

, продолжающее

. Однако существование такого отображения противоречит индукционному предположению.
Таким образом, мы доказали, что

. Предположим, что мы смогли доопределить

до непрерывного отображения

в

. По
теореме Брауэра существует

, такое что

. Так как

попадает в образ

, то

и

. Но это означает

и

. Противоречие.
 Лемма 2.
Лемма 2. Пусть

--- непрерывное отображение из

в

, такое что

и

для всех

. Тогда

.
Доказательство. Предположим противное. Пусть

не попадает в образ

. Так как непрерывный образ компакта замкнут, то

замкнуто и существует открытое множество, содержащее

и не пересекающееся с

. Пусть
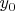
равно элементу

, находящемуся на полупрямой, выходящей из нуля и проходящей через

.
По лемме 1 имеем

. Для каждого

пусть

в случае

и

в противном случае. Тогда

обладает всеми нужными свойствами.
Далее. Если заменить

на

при достаточно большом

, то получим отображение из

в

, у которого все точки полуинтервала
![$(0,y_0]$ $(0,y_0]$](https://dxdy-02.korotkov.co.uk/f/1/4/2/142ed38dfc4dc74d83f87a597ff30ca082.png)
не содержатся в образе. После чего можно положить

при

и

при

. Отображение

удовлетворяет всем условиям леммы и справедливо
![$[0,y_0] \cap g_3(C^m_1) = \{ 0,y_0 \}$ $[0,y_0] \cap g_3(C^m_1) = \{ 0,y_0 \}$](https://dxdy-03.korotkov.co.uk/f/2/5/5/2551b93d401516aa84164ad33606334882.png)
.
Далее. Так как

, то

. В силу замкнутости

имеем

для некоторого

. Проделав теперь с

ту же процедуру, что мы проделали с

при построении

, можно "стянуть" весь шар

в ноль и получить отображение

, для которого

и которое обладает теми же свойствами, что и

.
Далее. Множество

замкнуто и не содержит

. Значит, найдётся

, такой что

. Для этого

найдётся

, такое что

. Положим

при

и

иначе. Получим непрерывное отображение

, которое удовлетворяет условию

и для которого

. А это, однако, противоречит лемме 1.

Вернёмся к исходной задаче. Пусть

--- отображение с требуемыми свойствами,

--- произвольный элемент

и

. Из второго условия существует

, такое что

. Пусть теперь

при

и

в противном случае. По выбору

имеем

. Кроме того,

непрерывно и

. По лемме 2 получаем

и

для некоторого

. А так как

, то и

также равно

. Что и требовалось доказать
