Zai писал(а):
R-o-m-e-n писал(а):
Заряд не индуцируется на внутренней поверхности сплошной сферы...
Если заряды связаны о каком индуцировании Вы говорите?
Заряды индуцируются при наличии поля в любом случае. Просто, когда они связаны, как в диэлектриках, они не перераспределяются и не компенсируют поле полностью, как в проводниках.
Zai писал(а):
Где в постановке задачи описывается сплошная сфера?
В однородно заряженной сфере радиуса
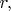
толщины

вырезали круглую дырочку диаметром

Т.е. заряжалась сплошная сфера, а потом в ней появилось отверстие.