Производная суммы не равна сумме производных

[ewert]

gris в сообщении #191935 писал(а):

Но если просто у гиперболы выкинуть часть, лежащую симметрично относительно нуля, то с учётом отрицательной площади слевва от нуля, интеграл будет давать приблизительно правильный ответ.

Да не будет он давать правильного ответа, поскольку такого ответа вообще не существует -- интеграл расходится. Если же имеется в виду его главное значение, то, во-первых, так надо честно и говорить и, во-вторых, никакая это не площадь.

[Xaositect]

ewert в сообщении #191919 писал(а):

TeX тут не при чём, просто Вы (видимо, из патриотизма) обозначили эту константу русской буквой.

Спасибо, исправил. Это единственная клавиша, которая дает одинаково выглядящие буквы на русской и английской раскладке.

[Brukvalub]

unnihilator в сообщении #191880 писал(а):

To Brukvalub:
А "морпех" - это не Ваш второй "НИК"?

Нет, просто я НЕНАВИЖУ разбушевавшееся ныне невежество, которое в лице таких, как вы все больше прет на форум со своими "математическими открытиями", не утруждая себя излишним математическим образованием.
Научился числа складывать, умножать и делить, узнал про формулы сокращенного умножения - и сразу сыпятся "загадочные" вопросы, вроде этих:

unnihilator в сообщении #191393 писал(а):

Имеем два куба, как функции от длины ребра (x), с объемами $V_1=x^3$ и $V_2=x^3+5$.

unnihilator в сообщении #191393 писал(а):

Кто ответит на вопрос: $\int_{-1}^e(\frac1x)dx$=?

unnihilator в сообщении #191393 писал(а):

А если начертить три гиперболы при $C_1=0,25$, $C_2=1$ и $C_3=9$, то что будет означать $ln1=0$?

Изумлю вас - ответить на такого рода вопросы вы легко сможете сами, если чуть-чуть подучитесь математике...

[unnihilator]

1. В формуле интегрирования по частям нет места никакой константе, потому, что ее тогда надо писать и слева и справа от "=", т.е. сумма констант при каждом интеграле должна быть равна суммарной константе при тензоре! Вы носитесь с этой абсурдной константой, не понимая, что:
- производная суммы не равна сумме производных, хотя я разложил вам это "по полочкам",
- прибавляя к функции некое значение в виде "C" вы просто создаете несколько иную зависимость значения функции от значения аргумента! И, если вы к функции площади круга от радиуса прибавите "С", то при одном и том же значении радиуса значение функции длины окружности от радиуса тоже будет зависеть от "C"!
$\int(2\pi r )dr +C=\pi R^2$, где$R$ находится по формуле $\int_r^R(2\pi r)dr=C$.$(\int(2\pi r )dr +C)'=(\pi R^2)'=2\pi R$ Вы "закопались" в формулах, не понимая, что они имеют отношение к ДЕЙСВТИТЕЛЬНОСТИ, а не служат для решения головоломок в виде дифуравнений, которым место в "Занимательной математике" или, на крайний случай, в разделе "головоломки для взрослых"!
To Xaositect:
1.Я попросил Вас привести ФОРМУЛУ, а не прочитать лекцию.
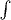
2. Посмотрите внимательно на Вашу формулу! В первом слагаемом сразу за значком "$\int$" стоит значок "$d$". Я думаю, Вам не надо объяснять, что такое " интеграл дифференциала"?

Добавлено спустя 15 минут 25 секунд:

Неопределенного интеграла $\int(\frac{1}{x})dx$ НЕ СУЩЕСТВУЕТ!!! Имеет место быть $\int_{x_1}^{x_2}(\frac{1}{x})dx=ln(\frac{x_2}{x_1})dx$ и он равен "0" в случае, когда $x_1=x_2$! Тогда все противоречия, возникающие всвязи с "разрывом" и "отрицательными значениями" исчезают и на вопрос $\int_{-1}^{e}(\frac{1}{x})dx=?$ формула дает ответ $ln(-(\frac{e}{1}))$ - НЕ СУЩЕСТВУЕТ!

[ewert]

unnihilator писал(а):

$\int(2\pi r )dr +C=\pi R^2$, где$R$ находится по формуле $\int_r^R(2\pi r)dr=C$.$(\int(2\pi r )dr +C)'=(\pi R^2)'=2\pi R$ Вы "закопались" в формулах,

Да уж, в Ваших формулах невозможно не закопаться, поскольку они лишены всякого смысла.

Конкретно здесь.
Первая формула совершенно бессмысленна хотя бы потому, что в левой части присутствует неопределённый интеграл, в то время как остальные слагаемые -- якобы вполне определённые.

Вторая (та, где Вы якобы находите $R$) -- безграмотна, т.к. $r$ не может быть одновременно и пределом, и переменной интегрирования.

С учётом этого третью можно б и не обсуждать, если б Вы не сделали там ещё одного математического открытия. Оказывается, с Вашей точки зрения совершенно безразлично, по какой переменной дифференцировать, главное -- просто штришок поставить.

[gris]

А собственно формула Ньютона-Лейбница

$\int_a^b f(x)dx= F(b)-F(a)$ тоже является частным случаем формулы Стокса. Точки $a$ и $b$ являются границей отрезка $[a;b]$ точно так же, как окружность является границей круга, а сфера границей шара.

А вообще формула Стокса выглядит так

$$\int \limits_{\sigma} d\omega = \int \limits_{\partial \sigma} \omega$$

[Mopnex]

Да уже всё ясно, человек из леса вышел и сразу всех поучать начал. Что либо объяснить ему не удастся. Готов держать пари.

[unnihilator]

Тогда еще разок:
1.$\int[2\sqrt(x^2+C)]d(\sqrt(x^2+C))=x^2+C$
2. $\int 2xdx=x^2+C$
Какой из этих двух вариантов верный?

Добавлено спустя 5 минут 19 секунд:

To ewert:
$\int_r^R(2\pi r)dr=C$ Вам не нравится, потому, что Вы не слышали о понятии "переменный предел интегрирования"? А теперь "услышали"? И чем это Вам не понравилось?

[gris]

Казалось бы оба верные, но функция

$\sqrt{x^2+C}$ при отрицательных $C$ определена на отрезке $|x|\geqslant \sqrt{-C}$, а $x^2+C$ определена при всех $x$.

Такие функции нельзя считать тождественно равными.

[unnihilator]

To ewert:
В приведенной выше формуле Стокса "$\sigma$" - это что?

[ewert]

unnihilator писал(а):

Тогда еще разок:
1.$\int[2\sqrt(x^2+C)]d(\sqrt(x^2+C))=x^2+C$
2. $\int 2xdx=x^2+C$
Какой из этих двух вариантов верный?

Второй верен, первый же -- безграмотен. Буквой $C$ справа обозначена произвольная постоянная, слева же -- параметр. Вы систематически не понимаете, что нельзя в одной и той же формуле разные объекты обозначать одним и тем же символом. Вот и ещё пример:

unnihilator писал(а):

To ewert:
$\int_r^R(2\pi r)dr=C$ Вам не нравится, потому, что Вы не слышали о понятии "переменный предел интегрирования"? А теперь "услышали"? И чем это Вам не понравилось?

Я всё слышал. А вот Вы -- не отдаёте себе отчёта в том, что сами же и написали. И не желаете вдумываться в то, что Вам говорят.

[gris]

А можно вперёд ewerta в пекло?

$\sigma$ это подмногообразие некоторого ориентируемого многообразия, а $\partial \sigma$ это его (сигминного) положительно ориентированная гранитса.

Не получилось поперёк-то

[ewert]

gris в сообщении #191998 писал(а):

это его (сигминного) положительно ориентированная гранитса.

Не годится, надо исправлять. Предлагаю на выбор:

"это её (сигменная) положительно ориентированная гранитса"

"это его (сигменный) положительно ориентированный гранитс"

[gris]

Я всегда сигму считал дамой. Неужели перепутал? Какой конфуз

Хотя под "его" я подразумевал "многообразие", так что правильно - ориентированное гранитсо.

[ewert]

Не конфузьтесь, там много вариантов, я просто не стал все перебирать. Вот ещё:

"это его (сигменная) положительно ориентированная гранитса"

"это её (сигменный) положительно ориентированный гранитс"