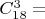проверьте

[Meteroka]

в козине имеется [21/6]+4 белых шаров, [21/6]+3 черных шаров и [21/6]+2 синих шаров. сколькими способами можно извлечь из корзины 3 шара так, что бы среди них черных шаров было больше чем синих?

1) два черных шара и 1 синий
C3 27=27!/3!(27-3)=27*26*25/3*2*1=2925
будет ли вариант когда ывнимаются все шары кроме синих?
подскажите, что еще нужно сделать

[Brukvalub]

Meteroka в сообщении #176644 писал(а):

подскажите, что еще нужно сделать

Перестать уродовать формулы и выказывать тем самым полное неуважение форуму.

[gris]

Meteroka, ну когда же Вы смиритесь, что у Вас 21-ый вариант и $[21/6] = 3, а [21/10] = 2$?
Перепишите условия с учётом этого, может быть тогда наступит прояснение?
Итак, в корзине 7 белых, 6 чёрных и 5 синих. Всего 18 шаров.

[Meteroka]

1) вынимаем 2 черных и 1 синий=2754
а будет ли вариан когда вынимаем все 3 черных шара?

[gris]

По условию, чёрных больше, чем синих. Синих может быть и 0. Ваш Вариант, скорее всего, ошибочен, но Вы можете настаивать на нём, утверждая, что раз чёрных шаров боольше, чем синих, то синие обязательно есть.
Но я бы рассмотрет такие варианты:
ЧЧЧ ЧЧС ЧЧБ ЧББ. Два средних просчитываются по одной формуле. Сколько всего вариантов?
Биномиальные коэффициенты записываются так: $C_{18}^{3}=$

[Meteroka]

спасибо большое!

Добавлено спустя 6 минут 46 секунд:

а в вух последних случаях биноминальные коэфициенты будут одинаковые?

[gris]

Постойте, я имел ввиду идею ЧЧC, а не то, как Вы её просчитали. У Вас какое-то безумное число.
Всего различных вариантов выбрать три шарика (в предположении, что они, между прочим как бы пронумерованы) $C_ {18}^{3} = 816$
А вариантов ЧЧС $C_ {6}^{2} \cdot C_ {5}^{1} = 75$
А то насоветую на Вашу голову, Вы и правда пойдёте с преподами воевать. Ну а дальше сами уж

[PAV]

[mod="PAV"]Тема перемещена в карантин. Почему это произошло, можно понять, прочитав тему
Что такое карантин и что нужно делать, чтобы там оказаться
Там же описано, как исправлять ситуацию.[/mod]

(формулы, неинформативный заголовок)