Аксиома выделения против доказательства теоремы Кантора

[cxzbsdhwert]

В известном доказательстве от обратного теоремы Кантора (она же вообще ещё доказывается как с последовательностями нулей и единиц, насколько я знаю) множество элементов отображающих в подмножества в которых они не содержатся полагается существующим по "аксиоме выделения".
То есть, если принять упомянутую аксиому, то теорема верна.

А что если, доказывая от обратного, то есть считая, что биекция $A\rightarrow 2^A$ существует, полагать, что такая биекция даже не одна, а их множество, и тогда по всё той же аксиоме выделения (принятие которой должно приводить к верность теоремы), среди множества биекций выделить подмножество тех биекций, в которых все элементы отображают только в подмножества в которых они содержатся? Ну и дальше применить те же соображения, которые теперь будут неверными, а значит утверждение от противного, по крайней мере по таким соображениям ложным не будет являться.

Получается противоречие - принятие аксиомы с одной стороны приводит к верности Теоремы, а с другой стороны неверности?

[mihaild]

То, что какое-то рассуждение, начинающиеся с предположения, не приводит к противоречию, еще не означает, что предположение верно.

[Mikhail_K]

cxzbsdhwert
Очень невнятно написано, напишите подробно и с формулами, чтобы было что обсуждать.

Имейте в виду вот что.

1) Рассуждать можно очень по-разному. Если в каком-то рассуждении получено противоречие, значит, принятое предположение было неверным - и это тем самым доказано. Но если при каком-то способе рассуждения противоречие НЕ получилось, то это не означает и не доказывает ничего - это не означает, что предположение верное. То есть если Вы предлагаете какой-то другой способ рассуждения и он не ведёт к противоречию (или Вы не видите как он ведёт к противоречию), то это просто ничего не доказывает и не опровергает. Это уже сказал mihaild.

2) Когда в доказательстве неравномощности $A$ и $2^A$ рассматривается "множество элементов отображающих в подмножества в которых они не содержатся" $\{x\in A\,|\,x\notin f(x)\}$, то НЕ имеется в виду, что такие элементы $x$ обязательно существуют. Если они не существуют, тогда множество будет пустым, но оно всё равно множество и на справедливость следующих рассуждений это не влияет.

3) Кстати! Легко понять, что не может существовать биекций $f:\,A\to 2^A$

cxzbsdhwert в сообщении #1718223 писал(а):

в которых все элементы отображают только в подмножества в которых они содержатся

(то есть для которых $\forall x\in A,\,x\in f(x)$). Дело в том, что среди подмножеств $A$ есть пустое множество, а раз $f$ биекция, то она должна отображать некоторый элемент $y\in A$ в пустое множество $\varnothing\in 2^A$. Тогда $f(y)=\varnothing$ и $y\notin f(y)$, так как $y\notin\varnothing$.

[cxzbsdhwert]

Mikhail_K в сообщении #1718226 писал(а):

Дело в том, что среди подмножеств $A$ есть пустое множество

Да, конечно
Но, согласитесь, что, по крайней мере, ограничиваясь рассмотрением данной Теоремы, утверждение о том что пустое множество является подмножеством любого множества несколько искусственно.
Вот что если доказывать эту Теорему полагая, что $\emptyset \not \in 2^A$?

Mikhail_K в сообщении #1718226 писал(а):

Очень невнятно написано

Да по-моему достаточно внятно, сложно придумать как ещё понятней.

Mikhail_K в сообщении #1718226 писал(а):

Если в каком-то рассуждении получено противоречие, значит, принятое предположение было неверным

Ну вот по-моему неверным является предположение о том, что при любой биекции можно выделить подмножество прообразов отображающих в образы, которым они не принадлежат, даже принимая аксиому выделения. Ну и, с условием что $\emptyset \not \in 2^A$ такое доказательство не получится. Я не спорю что можно доказать по другому.

[waxtep]

cxzbsdhwert в сообщении #1718228 писал(а):

Интуитивно это должны быть разные пустые множества.

В стандартной аксиоматике доказывается единственность пустого множества. Если Вы вводите другую аксиоматику, возможны различные самые интересные последствия и её тогда хорошо бы выписать полностью явно

[cxzbsdhwert]

waxtep
Что-то не припомню такого в курсе анализа. Наверное что-то в духе доказательства единственности нейтрального элемента в моноиде $e_1=e_1\circ e_2=e_2$ и тому подобных?

[mihaild]

cxzbsdhwert в сообщении #1718230 писал(а):

Что-то не припомню такого в курсе анализа

Теорию множеств в курсе анализа традиционно рассказывают отвратительно. Бывают исключения, но редко. И в целом она там на самом деле не особо нужна. Так что если вам по какой-то причине интересна теория множеств - её лучше изучать по специализированным источникам (например "Основы теории множеств" Верещагина и Шеня).

В ZF есть аксиома экстенсиональности: $\forall a \forall b ((\forall x: x\in a \leftrightarrow x \in b) \rightarrow A = B)$. Т.е. если множествам принадлежат одни и те же элементы, то множества равны. Выведите из этого, что любые два пустых множества равны.

[Mikhail_K]

cxzbsdhwert в сообщении #1718228 писал(а):

Но, согласитесь, что, по крайней мере, ограничиваясь рассмотрением данной Теоремы, утверждение о том что пустое множество является подмножеством любого множества несколько искусственно.

Не соглашусь. Это одно из базовых утверждений теории множеств, его не получится оттуда убрать, не разломав всю теорию.
Утверждение о том, что пустое множество есть подмножество любого другого - может выглядеть непривычно; ну так в математике много непривычного и неочевидного!

cxzbsdhwert в сообщении #1718228 писал(а):

Вот что если доказывать эту Теорему полагая, что $\emptyset \not \in 2^A$?

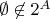
Полагать так будет неграмотно и неправильно, но я думаю, что я понял, о чём Вы спрашиваете. Вы хотите спросить, можно ли доказать отсутствие биекции между произвольным множеством $A$ и множеством его непустых подмножеств, т.е. множеством $2^A\backslash\{\varnothing\}$.

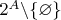
Ответ тут такой. Во-первых, утверждение об отсутствии биекции станет неверным для множеств $A$, состоящих из одного элемента, а также в случае $A=\varnothing$. В самом деле, если $A=\{a\}$, то в множестве $A$ один элемент и одно непустое подмножество (само $A$), и между ними взаимно-однозначное соответствие существует. Аналогично, если $A=\varnothing$, то у множества $A$ нет ни элементов, ни непустых подмножеств, и это тоже означает наличие взаимно-однозначного соответствия.

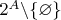
Во-вторых, для конечных множеств более чем из одного элемента, а также для бесконечных множеств, утверждение останется справедливым - не будет биекции между такими множествами $A$ и их множествами непустых подмножеств $2^A\backslash\{\varnothing\}$. Для конечных множеств это будет так потому, что если в множестве $A$ всего $n$ элементов, то непустых подмножеств у него будет $2^n-1$, а это строго больше чем $n$ при $n>1$.

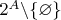
Для бесконечных множеств $A$ можно рассуждать так. Теорема Кантора утверждает неравномощность $A$ и $2^A$ (где $2^A$ включает пустое множество). Если $A$ бесконечно, то и $2^A$ бесконечно. Есть теорема, что при удалении одного элемента из бесконечного множества его мощность не меняется, так что $2^A\backslash\{\varnothing\}$ равномощно $2^A$ и, значит, неравномощно $A$.

cxzbsdhwert в сообщении #1718228 писал(а):

Да по-моему достаточно внятно, сложно придумать как ещё понятней.

Формулами, а не словами.

cxzbsdhwert в сообщении #1718228 писал(а):

Ну вот по-моему неверным является предположение о том, что при любой биекции можно выделить подмножество прообразов отображающих в образы, которым они не принадлежат, даже принимая аксиому выделения.

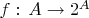
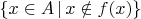
Если есть отображение $f:\,A\to 2^A$, то есть и множество $\{x\in A\,|\,x\notin f(x)\}$ - это просто факт. Уж будет ли это множество пустым или непустым - отдельный вопрос. Если интересует вопрос о существовании взаимно-однозначного соответствия между элементами $A$ и именно непустыми подмножествами $A$ - то да, рассуждать надо по-другому, например так как я написал выше.