Лемма о непрерывной биекции с другой точки зрения

[ChaosProcess]

Недавно читал современную статью с обсуждением оригинального доказательства теоремы Жордана о кривой (предложенного самим Жорданом). Там автор статьи использовал факт, что непрерывное инъективное отображение компактного кольца $S^1$ в евклидову плоскость является гомеоморфизмом. Ну и далее он использовал равномерную непрерывность обратного отображения из образа кривой, но это уже не суть важно. Обоснованием гомеоморфности является, например, простая лемма из общей топологии о том, что обратное отображение к непрерывной биекции компакта на Хаусдорфово пространство является непрерывным.

Мне стало интересно, как эту простую лемму можно доказать без использования общетопологического определения компактности через покрытия открытыми множествами. Все таки, когда Жордан опубликовал свое доказательство, этого определения еще не было, его немного позже ввел Борель. Вот, решил набросать свой вариант через секвенциальную компактность (поскольку речь идет о метрических пространствах, они эквивалентны). Прошу уважаемую общественность проверить правильность доказательства.

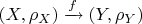
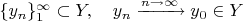
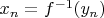
Итак, пусть задана непрерывная биекция метрических пространств $(X, \rho_X) \xrightarrow{f} (Y, \rho_Y)$, причем $X$ - секвенциально компактное пространство. Докажем, что $f^{-1}$ - непрерывная функция. Пусть задана произвольная сходящаяся последовательность $\{y_n\}_1^\infty\subset Y, \quad y_n \xrightarrow{n\to\infty} y_0\in Y$. Требуется показать, что последовательность $x_n = f^{-1}(y_n)$ сходится к точке $x_0 = f^{-1}(y_0)$.

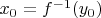
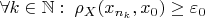
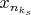
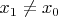
Действуем от противного, предположим, что $x_n$ не сходится к $x_0$. Это значит, что найдется число $\varepsilon_0>0$ и подпоследовательность $x_{n_k}$ такая, что $\forall k\in\mathbb{N}:\; \rho_X(x_{n_k}, x_0)\geq\varepsilon_0$. Из секв. компактности $X$ следует, что существует подпоследовательность $x_{n_{k_s}}$ последовательности $x_{n_k}$, сходящаяся к некоторой точке $x_1\neq x_0$. Из непрерывности и биективности $f$ следует, что $y_{n_{k_s}}=f(x_{n_{k_s}})\xrightarrow{s\to\infty}f(x_1)\neq f(x_0)=y_0$. 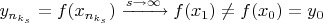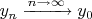Но это противоречит тому, что $y_n \xrightarrow{n\to\infty} y_0$ и равенству предела последовательности и подпоследовательности. $\qedsymbol$

[Mikhail_K]

ChaosProcess
Да, всё верно.

[ChaosProcess]

Mikhail_K в сообщении #1717753 писал(а):

ChaosProcess
Да, всё верно.

Ну и отлично. Интересно, сам Жордан это доказал на лету или тогда это уже был общеизвестный факт.