Вычисление SVD на компьютере: алгоритмы и литература

[B@R5uk]

Schrodinger's cat в сообщении #1712126 писал(а):

Мои реализации в 20 раз медленнее!

Вы не уточнили, на каком языке писали, чем компилировали и какого размера матрицы обсчитывали. Я подозреваю, что у вас дело в следующем. Современные процессоры поддерживают специальные инструкции для линейной алгебры, которые используют векторизацию вычислений, что даёт ускорение по сравнению с вычислением в цикле в десятки раз. По крайней мере для целочисленной арифметики такое точно есть. Возможно, вы не поставили в вашем компиляторе ключ, позволяющий использовать такие команды, либо он вообще не поддерживает их, либо ваш алгоритм написан так, что векторизовать его автоматически у компилятора не получается. Если обрабатываемые матрицы очень большие, то тут ещё выходит на сцену ограниченная скорость передачи данных между оперативной памятью и различными уровнями кэша процессора. Алгоритм должен быть составлен с учётом этих ограничений. У Голуба и Ван Лоана в книжке "Матричные вычисления" про последнее кое-что написано.

-- 27.01.2026, 11:26 --

zgemm в сообщении #1711360 писал(а):

Вам надо итерационно решать СЛАУ с регуляризацией, а именно

$$\min_x ||Ax - b||_2 + \lambda ||x||_2$$

и

$$\min_{x_t} ||A^T x_t - b_t||_2 + \lambda ||x_t||_2$$

Нет, мне надо находить решение системы

$$Ax=b$$

через псевдообратную матрицу

$$x=A^+b$$

SVD позволяет сделать это точно (при условии, что само SVD посчитано точно) и принять осведомлённое решение о степени вырожденности системы (определившись по какому-либо критерию, какие из слишком маленьких сингулярных значений считать нулевыми). То, что вы предлагаете даст приближённое решение, которое ещё и от левого параметра зависит. То, что мне нужно, получается из вашего при λ стремящимся к нулю.

Сейчас я пытаюсь думать несколько в другом направлении. Я тут недавно узнал "финт ушами", позволяющий вычислять псевдообратную матрицу через обычное матричное обращение. Для этого надо построить матрицу B, строки которой образуют базис (не обязательно ортогональный, но чем ближе к нему, тем лучше) подпространства, являющегося ортогональным дополнением к подпространству строк матрицы A, то есть

$$AB^T=0$$

Тогда если строки матрицы A линейно независимы, то её псевдообращение можно записать в виде

$$\begin{pmatrix}A^+&B^+\end{pmatrix}=\begin{pmatrix}A\\B\end{pmatrix}^{-1}$$

А решение исходной системы:

$$x=\begin{pmatrix}A\\B\end{pmatrix}^{-1}\begin{pmatrix}b\\0\end{pmatrix}$$

Фактически, строится дополненная матрица и от неё частично вычисляется обратная. Что именно можно выкинуть из алгоритмов обращения, мне надо ещё разбираться. Разумеется, матрицу B надо уметь выписывать явно, иначе весь смысл теряется. В этой ситуации, на сколько я понимаю, разреженность обращаемой матрицы должна дать временной выигрыш при вычислениях, тут мне тоже ещё надо разбираться.

[B@R5uk]

B@R5uk в сообщении #1716371 писал(а):

Сейчас я пытаюсь думать несколько в другом направлении.

Появилась тут ещё идея двигаться в третьем направлении: рассчитать псевдообращение недоопределённой матрицы A по её LU-разложению. Задача:

$$\lVert x\rVert\to\min,\qquad Ax=b,\qquad A\in\mathbb{R}^{m\times n},\qquad m<n,\qquad n-m\ll n$$

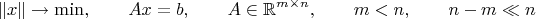
Матрицу A раскладываем с пивотированием по столбцам (P - перестановочная матрица):

$$AP=LU,\qquad x=Py,\qquad LUy=b,\qquad\lVert y\rVert=\lVert x\rVert\to\min$$

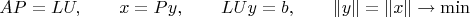
Расщепляем верхнедиагональную матрицу U на две половинки: квадратную (и поэтому обратимую) часть и всё остальное. Соответствующим же образом расщепляем и вектор y:

$$U=\begin{pmatrix}U_1&U_2\end{pmatrix},\qquad L,\;U_1\in\mathbb{R}^{m\times m},\qquad U_2\in\mathbb{R}^{m\times(n-m)}$$

$$y=\begin{pmatrix}y_1\\y_2\end{pmatrix},\qquad y_1\in\mathbb{R}^{m},\qquad y_2\in\mathbb{R}^{n-m}$$

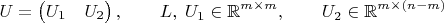
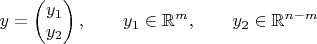
В результате получается:

$$U_1y_1+U_2y_2=L^{-1}b$$

$$y_1=U_1^{-1}L^{-1}b-U_1^{-1}U_2y_2$$

$$C=U_1^{-1}U_2$$

$$y=\begin{pmatrix}U_1^{-1}L^{-1}b\\0\end{pmatrix}+\begin{pmatrix}-C\\I_{n-m}\end{pmatrix}y_2$$

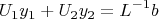
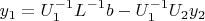
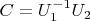
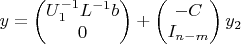
МНК решается стандартно по формуле:

$$\lVert y\rVert^2=y_2^TGy_2-2y_2^TC^TU_1^{-1}L^{-1}b+\left\lVert U_1^{-1}L^{-1}b\right\rVert^2\to\min$$

$$G=I_{n-m}+C^TC$$

$$y_2=G^{-1}C^TU_1^{-1}L^{-1}b$$

$$y=\begin{pmatrix}U_1^{-1}L^{-1}b\\0\end{pmatrix}+\begin{pmatrix}-C\\I_{n-m}\end{pmatrix}G^{-1}C^TU_1^{-1}L^{-1}b$$

$$x=P\begin{pmatrix}I_m-CG^{-1}C^T\\G^{-1}C^T\end{pmatrix}U_1^{-1}L^{-1}b$$

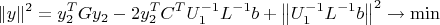
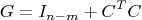
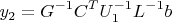
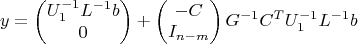
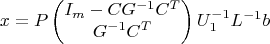
Поскольку размер симметричной матрицы G мал по сравнению с размером задачи (по условию), то трудозатраты на её обращение пренебрежимы по сравнению с LU-декомпозицией. При этом, если на единицу нормировать матрицу U, а не L (как это обычно делается, например в MATLAB'е), то вся некондиционность уйдёт в матрицу L (на сколько это возможно для этого разложения). Обращение квадратной половинки U даст матрицу с элементами, близкими к единице, а элементы второй её части будут меньше единицы. В результате число обусловленности матрицы G будет очень хорошее. Теоретически, нормировку столбцов U можно попытаться подобрать так, чтобы число обусловленности G стало ещё лучше, но это уже такие технические тонкости, о которых можно заботиться в самую последнюю очередь. Так же, есть надежда, что трудоёмкость задачи можно снизить, если воспользоваться тем, что матрица задачи разреженная.

В итоге, для псевдообращения A через её LU-разложение получается такая формула:

$$AP=L\begin{pmatrix}U_1&U_2\end{pmatrix},\qquad C=U_1^{-1}U_2,\qquad G=I_{n-m}+C^TC$$

$$A^+=P\begin{pmatrix}I_m-CG^{-1}C^T\\G^{-1}C^T\end{pmatrix}U_1^{-1}L^{-1}$$

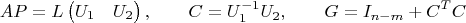
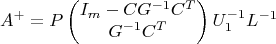
Возможно, её можно дальше упростить (есть у меня такие подозрения), надо будет покрутить формулы.

Этот подход к псевдообращению применительно к моей задаче имеет дополнительный бонус. Дело в том, что матрица A с числом строк и столбцов, соответственно

$$m=(D-1)N+1-\frac{D(D-1)}{2},\qquad n=(D-1)N+1,\qquad N\ge 2D$$

в моей задаче строится из первых (найденных) линейно независимых строк полной матрицы, у которой их

$$M=\frac{N(N-1)}{2}$$

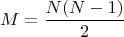
то есть много больше m для больших N. Сроки соответствуют линеаризированным связям, а их правильных выбор лежит в основе метода активного множества (в оптимизации). LU-разложение позволяет отбрасывать по мере нахождения линейно зависимые (с уже выбранными) строки и продолжать без потерь двигаться дальше. В результате одним выстрелом я убиваю сразу трёх зайцев:

1. Динамически нахожу активный набор связей;
2. Рассчитываю вектор-направление для итерации Ньютона;
3. Делаю это численно устойчивым методом (и, в потенциале, очень быстрым).

Надо теперь всё это реализовать и посмотреть что получается. Код на MATLAB'е, демонстрирующий работу формулы псевдообращения:

Используется синтаксис Matlab M

clc
clear all
format short
%format long

m = 6;
n = 10;

a = randn (m, n);

[u l p] = lu (a');
u = u';
l = l';
p = p';

u1 = u (:, 1 : m);
u2 = u (:, m + 1 : n);
u1_inv = u1 ^ -1;

b = u1_inv * l ^ -1;
c = u1_inv * u2;
g = c' * c + eye (n - m);

%disp (u1_inv)
%disp (c' * c)
%disp (' ')
%disp (svd (c)')
%disp (svd (g)')
disp (cond (c))
disp (cond (g))
disp (' ')

d1 = pinv (a);
d2 = [b; zeros(n - m, m)] + [-c; eye(n - m)] * g ^ -1 * c' * b;
d2 = p * d2;

disp (d1 - d2)
 

[B@R5uk]

B@R5uk в сообщении #1716436 писал(а):

Теоретически, нормировку столбцов диагонали/строк матрицы U можно попытаться подобрать так, чтобы число обусловленности G стало ещё лучше...

Это я глупость сморозил. Потому что, если

$$U'=\begin{pmatrix}U_1'&U_2'\end{pmatrix}=\begin{pmatrix}DU_1&DU_2\end{pmatrix}=DU$$

где D — некоторая невырожденная диагональная матрица, то

$$C'=U_1'^{-1}U_2'=U_1^{-1}D^{-1}DU_2=U_1^{-1}U_2=C$$

Таким образом, матрица G определяется только способом выбора поворотных элементов (пивотированием), ну, и выбором алгоритма тоже (QR-разложение даст другую верхнетреугольную матрицу).

[zgemm]

B@R5uk в сообщении #1716371 писал(а):

То, что мне нужно, получается из вашего при λ стремящимся к нулю.

далеко не всегда верное утверждение, если вы используете машинную арифметику, а в случае с итерационными методами - так вообще не верное, так как решая с лямбдой, можно ее использовать именно как отсечение по порогу.

Вы лучше спросите ИИ, он Вам расскажет, а я привык, что если кто-то что-то советует, то его во-первых, благодарят, во-вторых, вдумываются, почему именно такой совет был.

[B@R5uk]

zgemm, за наводку на разреженное LU и за указание, что SVD неизбежно приводит к заполнению — спасибо!