Наивные вопросы о формальных языках и грамматиках

[Anton_Peplov]

Здесь я буду задавать наивные вопросы о о формальных языках и грамматиках. Вопросы задаются по одному, следующий после закрытия предыдущего.

Вопрос № 1. Бывают ли в порождающих грамматиках правила с пустой левой частью?

Читаю две книги: Гладкий А. В. Формальные грамматики и языки. М.: Наука, 1987 и
Пентус А. Е, Пентус М. Р. Теория формальных языков. M.: Издательство Центра прикладных исследований при механико-математическом факультете МГУ, 2004.
Обнаружил расхождения в определениях.

Сначала изложу то, в чем согласны авторы обеих книг. Введем два непустых конечных множества $V$ и $W$, причем $V$ будем называть терминальным алфавитом, $W$ - вспомогательным алфавитом, $V \cup W$ - объединенным алфавитом. Кортеж элементов алфавита назовем цепочкой. Цепочка может быть и пустой. Правило порождающей грамматики - это упорядоченная пара цепочек объединенного алфавита $(\varphi, \psi)$, что записывается как $\varphi \to \psi$. Цепочки $\varphi$ и $ \psi$ называются, соответственно, левой и правой частями правила $\varphi \to \psi$.

Теперь расхождения. Пентусы (с. 6) требуют, чтобы левая часть правила была непустой цепочкой. У Гладкого (с. 27) я не обнаружил такого требования.

Вопрос: это два легитимных варианта терминологии? Если да, какой более распространен? Или же Гладкий просто забыл оговорить, что левая часть правила непуста? Иначе говоря, бывают ли в порождающих грамматиках правила с пустой левой частью?

Если я правильно понял идеологию порождающих грамматик, правила с пустой левой частью не нужны. Возможность вставить некоторую цепочку $\psi$ в любое место любой цепочки языка дает слишком много возможностей конструировать новые цепочки. Всего несколько таких правил - и мы получим $V^*$, множество всех возможных цепочек. Идея же порождающих грамматик родилась из исследования естественного языка, образующего весьма сложно устроенное подмножество $V^*$. Цель в том, чтобы найти в этой сложности максимально простую структуру. Если же нам нужно все $V^*$ или какое-нибудь его незамысловатое подмножество, есть другие способы его построить (символы вспомогательного алфавита в помощь). Но это мои дилетантские измышления, а я хочу знать, бывают ли правила с пустой левой частью "на самом деле", т.е. применяет ли их кто-нибудь где-нибудь.

[mihaild]

В определениях, которые я видел, обычно требуется непустота.
Но в целом - несложное упражнение: по грамматике, в которой есть правила с пустой правой частью, постройте грамматику, порождающую тот же язык, в которой таких правил уже нет.

[Anton_Peplov]

mihaild в сообщении #1715423 писал(а):

Но в целом - несложное упражнение: по грамматике, в которой есть правила с пустой правой частью, постройте грамматику, порождающую тот же язык, в которой таких правил уже нет.

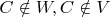
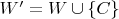
Пусть есть основной алфавит $V$, вспомогательный алфавит $W$ и грамматика $\Gamma$. Для начала расширим вспомогательный алфавит на один символ $C \notin W, C \notin V$. Получим новый вспомогательный алфавит $W' = W \cup \{C\}$. Теперь сделаем из грамматики $\Gamma$ грамматику $\Gamma'$ без правил с пустой левой частью.

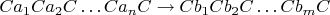
Идея в том, чтобы везде в левых и правых частях правил грамматики $\Gamma$ заменить все вхождения пустой цепочки на $C$. А именно, всякое правило грамматики $\Gamma$ с непустой левой и правой частью имеет вид $a_1 a_2 \dots a_n \to b_1 b_2 \dots b_m$, где $a_i$ - символы объединенного алфавита $V \cup W$. Заменим их на правила вида $Ca_1 Ca_2C \dots C a_n C \to C b_1 C b_2 C \dots C b_mC$. 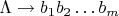Правила с пустой левой частью вида $\Lambda \to b_1 b_2 \dots b_m$, где $\Lambda$ - пустая цепочка, заменим на правила вида $\Lambda \to C b_1 C b_2 C \dots C b_mC$. 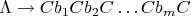Правила с пустой правой частью вида $a_1 a_2 \dots a_n \to \Lambda$ заменим на правила вида $Ca_1 Ca_2C \dots C a_n C \to C$.

Добавим в $\Gamma'$ еще два правила:
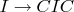
1) $I \to C I C$, где $I$ - начальный символ. Это правило нужно, чтобы вывести левую часть любого правила $\Gamma'$ из начального символа.
2) $C \to \Lambda$. Это правило нужно, чтобы на последнем шаге вывода устранить вспомогательный символ $C$.

Докажем, что грамматики $\Gamma$ и $\Gamma'$ порождают один и тот же язык. Рассмотрим произвольный полный вывод в грамматике $\Gamma$:
$D = (I, a_1 a_2 \dots a_n, b_1 b_2 \dots b_m, \dots, z_1 z_2 \dots z_k)$
Ему соответствует полный вывод в грамматике $\Gamma'$:
$D' = (I, CIC, C a_1 C a_2 C \dots C a_n C , C b_1 C b_2 C \dots C b_m C, \dots, C z_1 C z_2 C \dots C z_k, z_1 z_2 \dots z_k)$.
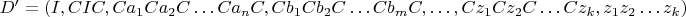
Обратно, любой полный вывод в грамматике $\Gamma'$ имеет вид $D'$, и ему соответствует полный вывод $D$ в грамматике $\Gamma$.

Вот теперь, кажется, все правильно.

[mihaild]

Можно попроще. $C$ у нас будет служить вспомогательным символом, заменяющим "пустую строку". Во всех правилах правую часть вида $a_1\ldots a_n$ заменим на $Ca_1Ca_2\ldotsCa_nC$, и добавим правило $C \to \Lambda$. При преобразовании старого вывода в новый, поддерживаем инвариант "текущая строка в новой грамматике - это текущая строка в старой грамматике, в которой вокруг всех сиволов поставили $C$", при применении правила в старой грамматике - стираем лишние $C$ и применяем правило. При обратном преобразовании поддерживаем инвариант "текущая строка в старой грамматике получается из текущей строки в новой вычеркиванием $C$".