Разложение полинома в сумму квадратов

[YuryS]

Добрый день !

Есть такой вопрос - дан многочлен от нескольких переменных с целочисленными коэффициентами $h\in \mathbb{Z}[x_{1}, ... , x_{n}]$.
Требуется разложить его в сумму квадратов двух аналогичных полиномов $f$ и $g$, т.е., $h = f^{2} + g^{2}$.
Эту задачу можно решать общим методом, пытаясь найти разложение исходного полинома $h$ в произведение двух полиномов в (факториальном) кольце гауссовых полиномов, т.е., ища разложение $h = (f + ig)(f-ig) $.
Однако, для больших полиномов h системы компьютерной алгебры вычисляют такое разложение бесконечно долго - например, полином от 6 переменных с общей степенью 28 главного монома считался сутки, но не дал результата.
Существуют ли быстрые алгоритмы решения этой задачи специальными, именно для этой задачи предусмотренными , методами ?
Различные ИИ (LLMs) не дают ответа на этот вопрос.

[Alex Krylov]

По запросу SOS Programming не искали?

[dgwuqtj]

Я не уверен, что в общем случае это сильно проще, чем факторизация. Но вообще алгоритмы в системах компьютерной алгебры могут быть не самыми оптимальными. Например, если вы изначально не уверены, что многочлен раскладывается в сумму квадратов, можно провести для этого отдельные быстрые тесты.

[YuryS]

Alex Krylov в сообщении #1714886 писал(а):

По запросу SOS Programming не искали?

По этой теме , в основном, ответы по оптимизации, т.е., про полиномы с вещественными коэффициентами. Задача же стоит про полиномы с целочисленными коэффициентами, т.е., это область диофантовых уравнений.

-- Чт янв 15, 2026 16:57:08 --

dgwuqtj в сообщении #1714887 писал(а):

Я не уверен, что в общем случае это сильно проще, чем факторизация.

Я общим случаем называю как раз факторизацию - разложение в произведение.
Интересует же (алгоритмическое) решение именно специальной задачи - разложения на сумму квадратов.

[Alex Krylov]

Есть вот такая, например, штука (лично не пробовал):
SPECTRA – a Maple library for solving linear matrix inequalities in exact arithmetic
https://www.unilim.fr/pages_perso/simone.naldi/papers/2017_spectra.pdf
Один из авторов, Didier Henrion, видный представитель в данной области (SOS).

Т.е., если задача небольшой(!) размерности, можно попробовать получить "exact certificate of SOS-representability or NON-representability"

[YuryS]

Alex Krylov в сообщении #1714944 писал(а):

SPECTRA – a Maple library for solving linear matrix inequalities in exact arithmetic

Да, спасибо, поизучаю.

[Alex Krylov]

Я вот что имею в виду...

Пусть $p$ - многочлен, для которого нам надо получить SOS-представление или удостовериться, что оно существует. Пусть $v$ - вектор мономов. Тогда должно выполняться $p=v^T Q v$, где симметричная матрица $Q$ должна быть неотрицательно определенной. Вот это $p=v^T Q v$ означает, кто коэффициенты при мономах должны быть равны, т.е. имеем систему линейных ограничений в форме равенств, от которых избавляемся, находя общее решение СЛАУ и подставляя его в $P$. В результате имеем одно линейное матричное неравенство, для которого надо решить "feasibility problem".

И якобы вышеуказанная программулька (для задач небольшой размерости) может проделывать подобные вещи в явной арифметике.

[Rak so dna]

Alex Krylov в сообщении #1715032 писал(а):

И якобы вышеуказанная программулька (для задач небольшой размерости) может проделывать подобные вещи в явной арифметике.

И, скорее всего, будет выглядеть это примерно так. А ведь это всего лишь полином шестой степени трёх переменных.

[Alex Krylov]

Rak so dna
Спасибо за наводку! Функционал Mathematica впечатляет.

Правда, к сож. алгоритмического описания не приводится: https://reference.wolfram.com/language/ref/PolynomialSumOfSquaresList.html

[YuryS]

Rak so dna в сообщении #1715040 писал(а):

И, скорее всего, будет выглядеть это примерно так

Что-то я не понял - что я сделал не так ?
Mathematica просто почленно разложила исходный полином
https://www.wolframcloud.com/obj/3ea406 ... 65f88d4779

[Rak so dna]

Добавьте

Total[%^2//Factor]

https://www.wolframcloud.com/obj/75f4dbd6-a39b-418e-a570-37c9c3b8f82f

[YuryS]

Rak so dna в сообщении #1715120 писал(а):

Добавьте Код:

Total[%^2//Factor]

Да, спасибо, так стало понятно (правда , ссылка https://www.wolframcloud.com/env/55e217 ... dabae279b4 недоступна - "Sorry, you do not have permission to access this item.").

Но остался непонятным главный вопрос - как эта функция из Mathematic'и может помочь в поиске разложения с целыми коэффициентами ?

Дело в том, что ИИ GLM-4.7 предложил пару идей, которые при доработке удалось реализовать с помощью системы SymPy на Python,
и полученный алгоритм исключительно быстро и корректно работает (проверено уже на десятках полиномов).
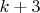
Так, например, полином $k$, который предлагался Mathematic'е (https://www.wolframcloud.com/obj/3ea406 ... 65f88d4779) он разложил за 0,05 сек, а про полином $k + 3$ он сказал, что такое разложение невозможно за 0,2 сек. :

/SymPy$ python main.py

h :  9*u**10*v**2*x**8*y**2*z**6 - 6*u**7*v**3*w**5*x**5*y*z**4 + 12*u**6*v**5*w**2*x**6*y**3*z**3 - 42*u**5*v**4*x**5*y*z**4 - 78*u**5*v*w*x**7*y**3*z**4 + 6*u**5*v*x**6*y*z**6 - 6*u**5*v*x**4*y**7*z**8 + 66*u**5*v*x**4*y*z**3 + 4*u**4*v**14*w**6*x**2*y**2*z**2 + u**4*v**4*w**10*x**2*z**2 - 4*u**3*v**8*w**4*x**2*y**2*z**2 - 4*u**3*v**6*w**7*x**3*y**2*z + 4*u**2*v**9*w**4*x*y**2*z**2 + 4*u**2*v**8*w**4*x**4*y**4 - 4*u**2*v**7*w**5*x**2*y**4*z**2 + 44*u**2*v**7*w**3*x**3*y*z**2 - 24*u**2*v**7*w**3*x**2*y**2*z**2 + 4*u**2*v**7*w**3*x*y**8*z**6 + 4*u**2*v**7*w**3*x*y*z**4 + 8*u**2*v**7*w**3*x*y*z + 14*u**2*v**5*w**5*x**2*z**2 + 26*u**2*v**2*w**6*x**4*y**2*z**2 - 2*u**2*v**2*w**5*x**3*z**4 + 2*u**2*v**2*w**5*x*y**6*z**6 - 22*u**2*v**2*w**5*x*z + u**2*v**2*w**2*x**2*y**2*z**2 - 28*u*v**7*w**2*x**3*y**2*z - 52*u*v**4*w**3*x**5*y**4*z + 4*u*v**4*w**2*x**4*y**2*z**3 - 4*u*v**4*w**2*x**2*y**8*z**5 + 44*u*v**4*w**2*x**2*y**2 - 2*u*v**3*w**2*x*y**2*z**2 + 2*u*v*w**3*x**2*y**4*z**2 - 22*u*v*w*x**3*y*z**2 + 12*u*v*w*x**2*y**2*z**2 - 2*u*v*w*x*y**8*z**6 - 2*u*v*w*x*y*z**4 - 4*u*v*w*x*y*z + 49*v**6*x**2*z**2 + v**4*w**2*y**2*z**2 + 182*v**3*w*x**4*y**2*z**2 - 14*v**3*x**3*z**4 + 14*v**3*x*y**6*z**6 - 154*v**3*x*z - 2*v**2*w**3*x*y**4*z**2 + 22*v**2*w*x**2*y*z**2 - 12*v**2*w*x*y**2*z**2 + 2*v**2*w*y**8*z**6 + 2*v**2*w*y*z**4 + 4*v**2*w*y*z + w**4*x**2*y**6*z**2 + 169*w**2*x**6*y**4*z**2 - 22*w**2*x**3*y**3*z**2 + 12*w**2*x**2*y**4*z**2 - 2*w**2*x*y**10*z**6 - 2*w**2*x*y**3*z**4 - 4*w**2*x*y**3*z - 26*w*x**5*y**2*z**4 + 26*w*x**3*y**8*z**6 - 286*w*x**3*y**2*z + x**4*z**6 + 121*x**4*z**2 - 132*x**3*y*z**2 + 22*x**2*y**7*z**6 - 2*x**2*y**6*z**8 + 36*x**2*y**2*z**2 + 22*x**2*z**4 + 22*x**2*z**3 + 44*x**2*z - 12*x*y**8*z**6 - 12*x*y*z**4 - 24*x*y*z + y**14*z**10 + y**12*z**10 + 2*y**7*z**8 + 4*y**7*z**5 - 22*y**6*z**5 + z**6 + 4*z**3 + 125

F :  2*u**2*v**7*w**3*x*y*z - u*v*w*x*y*z + v**2*w*y*z - w**2*x*y**3*z + 11*x**2*z - 6*x*y*z + y**7*z**5 + z**3 + 2
G :  3*u**5*v*x**4*y*z**3 - u**2*v**2*w**5*x*z + 2*u*v**4*w**2*x**2*y**2 - 7*v**3*x*z - 13*w*x**3*y**2*z + x**2*z**3 - y**6*z**5 + 11

SUCCESS !
ELAPSED TIME :  0.05415749549865723   sec.

/SymPy$ python main.py

h :  9*u**10*v**2*x**8*y**2*z**6 - 6*u**7*v**3*w**5*x**5*y*z**4 + 12*u**6*v**5*w**2*x**6*y**3*z**3 - 42*u**5*v**4*x**5*y*z**4 - 78*u**5*v*w*x**7*y**3*z**4 + 6*u**5*v*x**6*y*z**6 - 6*u**5*v*x**4*y**7*z**8 + 66*u**5*v*x**4*y*z**3 + 4*u**4*v**14*w**6*x**2*y**2*z**2 + u**4*v**4*w**10*x**2*z**2 - 4*u**3*v**8*w**4*x**2*y**2*z**2 - 4*u**3*v**6*w**7*x**3*y**2*z + 4*u**2*v**9*w**4*x*y**2*z**2 + 4*u**2*v**8*w**4*x**4*y**4 - 4*u**2*v**7*w**5*x**2*y**4*z**2 + 44*u**2*v**7*w**3*x**3*y*z**2 - 24*u**2*v**7*w**3*x**2*y**2*z**2 + 4*u**2*v**7*w**3*x*y**8*z**6 + 4*u**2*v**7*w**3*x*y*z**4 + 8*u**2*v**7*w**3*x*y*z + 14*u**2*v**5*w**5*x**2*z**2 + 26*u**2*v**2*w**6*x**4*y**2*z**2 - 2*u**2*v**2*w**5*x**3*z**4 + 2*u**2*v**2*w**5*x*y**6*z**6 - 22*u**2*v**2*w**5*x*z + u**2*v**2*w**2*x**2*y**2*z**2 - 28*u*v**7*w**2*x**3*y**2*z - 52*u*v**4*w**3*x**5*y**4*z + 4*u*v**4*w**2*x**4*y**2*z**3 - 4*u*v**4*w**2*x**2*y**8*z**5 + 44*u*v**4*w**2*x**2*y**2 - 2*u*v**3*w**2*x*y**2*z**2 + 2*u*v*w**3*x**2*y**4*z**2 - 22*u*v*w*x**3*y*z**2 + 12*u*v*w*x**2*y**2*z**2 - 2*u*v*w*x*y**8*z**6 - 2*u*v*w*x*y*z**4 - 4*u*v*w*x*y*z + 49*v**6*x**2*z**2 + v**4*w**2*y**2*z**2 + 182*v**3*w*x**4*y**2*z**2 - 14*v**3*x**3*z**4 + 14*v**3*x*y**6*z**6 - 154*v**3*x*z - 2*v**2*w**3*x*y**4*z**2 + 22*v**2*w*x**2*y*z**2 - 12*v**2*w*x*y**2*z**2 + 2*v**2*w*y**8*z**6 + 2*v**2*w*y*z**4 + 4*v**2*w*y*z + w**4*x**2*y**6*z**2 + 169*w**2*x**6*y**4*z**2 - 22*w**2*x**3*y**3*z**2 + 12*w**2*x**2*y**4*z**2 - 2*w**2*x*y**10*z**6 - 2*w**2*x*y**3*z**4 - 4*w**2*x*y**3*z - 26*w*x**5*y**2*z**4 + 26*w*x**3*y**8*z**6 - 286*w*x**3*y**2*z + x**4*z**6 + 121*x**4*z**2 - 132*x**3*y*z**2 + 22*x**2*y**7*z**6 - 2*x**2*y**6*z**8 + 36*x**2*y**2*z**2 + 22*x**2*z**4 + 22*x**2*z**3 + 44*x**2*z - 12*x*y**8*z**6 - 12*x*y*z**4 - 24*x*y*z + y**14*z**10 + y**12*z**10 + 2*y**7*z**8 + 4*y**7*z**5 - 22*y**6*z**5 + z**6 + 4*z**3 + 128
FAILURE !
ELAPSED TIME :  0.20119547843933105   sec.

Если есть желание проверить алгоритм на каком-нибудь трудном полиноме, то можно разместить или присоединить его здесь.
Единственное пожелание - порядок на переменных должен быть лексикографическим : a > b > ... > u > v > w > x > y > z ( использование собственного порядка имеет некоторые неудобства).

[dgwuqtj]

Можно ещё взять и реализовать самому что-то типа этого.

[Rak so dna]

YuryS в сообщении #1715123 писал(а):

Если есть желание проверить алгоритм на каком-нибудь трудном полиноме, то можно разместить или присоединить его здесь.

Попробуйте это:

(Оффтоп)

248775988341732950858056557430888155310287412851883988490100804*y^14*z^10+39894439281257203125108708758175536064159144646320880798088289*y^12*z^10-
76967932720138938430343364237015314591386355404229783737248*u^5*v*x^4*y^7*z^8+145494139341124631351398580260139637818829447673160938161436384*y^7*z^8-
208946026502591947118082475870540211106541365756060812417913882*x^2*y^6*z^8-712812980068826636912114353171379664885759506518548811750717112*w^2*x*y^10*z^6+
1121795117623477186771304717710480173796931641771728824865833394*w*x^3*y^8*z^6+21039611832354766162571128356427470069170819681883191234066540*u^2*v^7*w^3*x*y^8*
z^6-276917681622583044532701308570195215535010381867088403362608920*u*v*w*x*y^8*z^6-266617126587930991568238570833004076171956280220509578996714396*x*y^8*z^6+
266617126587930991568238570833004076171956280220509578996714396*v^2*w*y^8*z^6+48215643439181966366992875120711266888542054268978751342434816*x^2*y^7*z^6+
1499968284561788473839474342029993322312238102407692900001987912*u^2*v^2*w^5*x*y^6*z^6+2909951567181530062324366573526357060602617594083385181716*v^3*x*y^6*z^6+
37123360886507162011637498809864074669081346169253193984*u^10*v^2*x^8*y^2*z^6+201558713441391975812779309473811333145386235918579505550112*u^5*v*x^6*y*z^6+
273587264151203513910662852202481206906035845047021846162713929*x^4*z^6+21272696697657436814097444571134082072784174465473938772734016*z^6-
24002184945997434532202300953333226702475195351314511374978634*u*v^4*w^2*x^2*y^8*z^5+5217736752153232908738802653735224929948520383243056532543754909924*y^7*z^5
-392202694868094120590682469869010297116025434615410178332598834*y^6*z^5-1082133910070877609657980429743791245859858728329377344710304*u^5*v*w*x^7*y^3*z^4-
208440757762831207944998033002035969866517729888870390963590176*w^2*x*y^3*z^4-2937685509563662428608090927502079277793193568646193981920794186*w*x^5*y^2*z^4-
1446936717101990140456733717848880090693882291201628057854592*u^7*v^3*w^5*x^5*y*z^4-2807069863329493522807648261528297230902514083638971456*u^5*v^4*x^5*y*z^4+
6152402882658517050168737584687154768211114649776500653139920*u^2*v^7*w^3*x*y*z^4-80976263072207697191868877111829820872957107356131405075136160*u*v*w*x*y*z^4-
77964174969388205749801972993542900048272051957428694652891408*x*y*z^4+77964174969388205749801972993542900048272051957428694652891408*v^2*w*y*z^4-
3928021280478793992915840551881406595304887416838078644920085928*u^2*v^2*w^5*x^3*z^4-7620395576824487468066412271701426120311774776003920598404*v^3*x^3*z^4+
14099217516374587247410389452770952819940170906767106741229568*x^2*z^4+23153584676747018090214006093859038254368651704831459994144*u^6*v^5*w^2*x^6*y^3*z^3+
62855391154760070491917293767715575101458123144106337505215746*u*v^4*w^2*x^4*y^2*z^3+378336319235433033629578067464431345554598428802108002717344*u^5*v*x^4*y*z^3
+1027075403899677167678348998470082307453419151518728590638009546*x^2*z^3+1525770479545392153313476574737547047141830969159714193991939443952*z^3+
510602277114303882127165772231800795817815383478012059467604484*w^4*x^2*y^6*z^2+7885962985041194865951976677263736266043694917568088170668385681*w^2*x^6*y^4*z^2-
30142194408873144397963219342384323219272283338865143455667060*u^2*v^7*w^5*x^2*y^4*z^2+396723412068203791913634195688377391180699184578317384113203880*u*v*w^3*
x^2*y^4*z^2+381966422497877200516917029211330060177313867818753447501794244*w^2*x^2*y^4*z^2-381966422497877200516917029211330060177313867818753447501794244*v^2*
w^3*x*y^4*z^2-69075670676481046167611078487745058979296646608700742499546624*w^2*x^3*y^3*z^2+21088867628251207500995433114636912995467727364949659259163930376*
u^2*v^2*w^6*x^4*y^2*z^2+40912587310365569173698645712269522801748272841327613815668*v^3*w*x^4*y^2*z^2+444843239300181484543179568655270556354083369680527587953225*
u^4*v^14*w^6*x^2*y^2*z^2-11709812851494916796262988937885183208523888548416932302772100*u^3*v^8*w^4*x^2*y^2*z^2-
11274240911792303247794006678481213386391656867170781873192730*u^2*v^7*w^3*x^2*y^2*z^2+77060695152268425754588004015105814867471429850607438652892900*u^2*v^2*w^2*
x^2*y^2*z^2+148388510217043351123139109209923407525897482570578947488043540*u*v*w*x^2*y^2*z^2+71434438532265836054173565507098045348983016410003338025557601*x^2
*y^2*z^2+11274240911792303247794006678481213386391656867170781873192730*u^2*v^9*w^4*x*y^2*z^2-148388510217043351123139109209923407525897482570578947488043540*u*
v^3*w^2*x*y^2*z^2-142868877064531672108347131014196090697966032820006676051115202*v^2*w*x*y^2*z^2+71434438532265836054173565507098045348983016410003338025557601
*v^4*w^2*y^2*z^2+2038859194107834501297864266994683647749245777129378244366080*u^2*v^7*w^3*x^3*y*z^2-
26834913385568844520667990748349964486901886079560154423651840*u*v*w*x^3*y*z^2-25836730457853509640814246597668625578666969421854294614452992*x^3*y*z^2+
25836730457853509640814246597668625578666969421854294614452992*v^2*w*x^2*y*z^2+2336186349565340262756358376138530670642923798525946354876416*x^4*z^2+
14099113154776571194797421186058191155046734319773396869164299024*u^4*v^4*w^10*x^2*z^2+54704805218728938478188495829717616705609318868366139322064*u^2*v^5*w^5*x^2*
z^2+53063899856091638648741108670288823200655924519515876*v^6*x^2*z^2-337459735865563650932326994393342713475539485215075974183429882*u*v^4*w^3*x^5*y^4*z-
7475139599099860901171476001636532455698487186084800391141333730236*w^2*x*y^3*z-451222235827950197766154155665345229789265148174322202879839336*u^3*v^6*w^7*x^3*
y^2*z-875375076799238504797219547284388298800095411049652270948*u*v^7*w^2*x^3*y^2*z-5514190400321042707584890128628856072409645990358326126818584482*w*x^3*y^2*z
+220638568538046663951771633742297798841059159979215359713489768870*u^2*v^7*w^3*x*y*z-2903985176291299864885680585213378108987672489370216289322205713260*u*
v*w*x*y*z-2795965135992931076880754384669625293528797520427465986028009680638*x*y*z+2795965135992931076880754384669625293528797520427465986028009680638*
v^2*w*y*z+505628651057263018670498222460855939328188718445033721350832059648*x^2*z-7373102793528806830381729696734282530992063190230051564903760136*u^2*v^2*
w^5*x*z-14303883788641434808994130234199681134210732831147637215348*v^3*x*z+3610182851050406695932107167707591617580996908680345943863801*u^2*v^8*w^4*x^4*y^4+
117982879169895392558648103326389633213374172656894263499598202*u*v^4*w^2*x^2*y^2+27358727379057660907676454783634697108147320855814000010993162368272562

-- 17.01.2026, 21:57 --

YuryS в сообщении #1715123 писал(а):

про полином $k + 3$ он сказал, что такое разложение невозможно за 0,2 сек.

Это легко показать, поскольку для $k(x,y,z,u,v,w)$ имеем $k(1,1,1,1,-1,1)+3=76$, которое не представимо суммой квадратов двух целых чисел.

[YuryS]

dgwuqtj в сообщении #1715128 писал(а):

Можно ещё взять и реализовать самому что-то типа этого
.

Спасибо. Подход предложенный ИИ - в точности тот, который описан в этой статье (пока просто по абстракту) только с заменой слова "rational" на "integer" и "rationality" на "integrality" , но без "ladder-like", поскольку никакие матрицы не используются:
" ... our approach ensures that all coefficients in the decomposition remain rational. This is particularly useful in formal verification and symbolic computation, where exact arithmetic is required. We introduce a stepwise reduction technique that transforms a given polynomial into a sum of ladder-like squares while preserving rationality.