Псевдопростые в PARI/gp

[Yadryara]

Давно интересовал этот вопрос, спрашивал у Qwena, но до сих пор не знаю на него ответа.

Dmitriy40 в сообщении #1714988 писал(а):

Здесь есть вероятность пропуска решения (ошибки ispseudoprime, может вернуть true на составном числе), очень маленькая, сильно меньше $10^{-13}$, но есть.

Охота узнать, а каково же минимальное исключение? Для начала, может ли кто-то предъявить хотя бы одно число, которое современная версия PARI (от 2.15) объявит псевдопростым, а оно на самом деле составное?

[mathpath]

В Go функция ProbablyPrime предназначена для работы с большими целыми числами (big.Int). Она реализует тест Миллера-Рабина.
В расте в пакете num-bigint есть метод .is_probable_prime(millis_rabin_iterations) для типа BigUint, который полностью аналогичен Go-шной ProbablyPrime.

Если тест говорит "составное" — число точно составное (детерминированный результат).
Если тест говорит "вероятно простое" — есть ничтожно малая вероятность, что число на самом деле составное (так называемое псевдопростое число).

Вероятность того, что составное число будет k раз подряд признано "вероятно простым" тестом Миллера-Рабина, строго меньше, чем (1/4)^k.
В криптографии обычно используют k = 40-64
В общем случае k = 10-25 более чем достаточно.
Числа Кармайкла тест Миллера-Рабина надежно выявляет за несколько итераций.

[Yadryara]

mathpath, Спасибо. Лично мне, например, почти всё что Вы сказали было известно. Прошу рассматривать эту тему не как вопрос в ПР/Р, а как своего рода конкурс. Кто сможет предъявить такое число?

[Dmitriy40]

Yadryara в сообщении #1715038 писал(а):

Охота узнать, а каково же минимальное исключение? Для начала, может ли кто-то предъявить хотя бы одно число, которое современная версия PARI (от 2.15) объявит псевдопростым, а оно на самом деле составное?

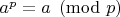
Надо различать ispseudoprime(x) и ispseudoprime(x,1) - они работают существенно по разному. И я говорил про вторую, с 1 вторым параметром. В таком формате она выполняет одну итерацию теста Миллера-Рабина, т.е. фактически одну проверку теста Ферма, условие $a^p = a\pmod p$ для произвольного $a$. А как известно числа Кармайкла и являются исключением для теста Ферма. И при случайном выборе $a$ тест может когда-нибудь на них наткнуться. Вот например на каких итерациях подряд натыкается при проверке наименьшего числа Кармайкла и наименьшего сильно псевдопростого числа по основанию 2:

? for(i=1,1000, if(ispseudoprime(561,1), print1(i,", ")))
3, 19, 156, 259, 282, 341, 399, 419, 427, 431, 485, 575, 592, 621, 679, 778, 826, 834, 913, 974,
? for(i=1,1000, if(ispseudoprime(561,1), print1(i,", ")))
112, 217, 263, 390, 392, 463, 523, 539, 580, 584, 611, 663, 678, 680, 978,
? for(i=1,1000, if(ispseudoprime(561,1), print1(i,", ")))
40, 88, 382, 519, 545, 643, 645, 674, 782, 799, 813, 829, 838, 878, 888,
? for(i=1,1000, if(ispseudoprime(2047,1), print1(i,", ")))
16, 17, 36, 43, 48, 50, 55, 59, 60, 79, 82, 83, 97, 144, 174, 202, 208, 211, 213, 232, 239, 243, 245, 247, 251, 255, 271, 273, 293, 295, 300, 306, 317, 328, 343, 345, 352, 362, 373, 374, 382, 383, 385, 395, 404, 426, 433, 434, 435, 468, 480, 483, 484, 487, 494, 500, 507, 526, 534, 535, 546, 552, 554, 564, 565, 570, 574, 576, 594, 596, 606, 610, 612, 615, 620, 622, 633, 649, 671, 674, 677, 681, 687, 689, 698, 700, 704, 720, 723, 726, 727, 761, 766, 772, 773, 781, 815, 819, 821, 824, 827, 834, 837, 839, 857, 860, 901, 904, 906, 907, 912, 925, 933, 940, 945, 967, 973, 988, 991, 993, 998,
? for(i=1,1000, if(ispseudoprime(2047,1), print1(i,", ")))
22, 34, 37, 41, 44, 53, 75, 100, 104, 108, 109, 114, 124, 130, 132, 158, 165, 168, 189, 201, 242, 245, 260, 271, 279, 299, 310, 316, 338, 346, 350, 353, 355, 359, 361, 363, 366, 374, 376, 385, 395, 404, 411, 417, 420, 424, 431, 448, 458, 465, 493, 494, 517, 522, 529, 534, 546, 552, 563, 582, 583, 585, 594, 595, 598, 599, 604, 615, 619, 623, 624, 648, 657, 664, 668, 690, 703, 706, 713, 714, 717, 723, 725, 731, 732, 736, 737, 739, 748, 761, 772, 773, 794, 797, 812, 827, 834, 839, 840, 844, 853, 854, 856, 892, 896, 899, 901, 918, 919, 920, 940, 944, 955, 964, 971, 982, 995,
? for(i=1,1000, if(ispseudoprime(341,1), print1(i,", ")))
15, 16, 22, 47, 68, 73, 76, 77, 79, 87, 88, 95, 97, 110, 116, 123, 129, 132, 134, 136, 139, 149, 156, 158, 162, 164, 174, 181, 184, 188, 189, 192, 198, 204, 214, 215, 228, 233, 245, 247, 248, 251, 255, 260, 261, 262, 263, 269, 273, 290, 296, 299, 305, 310, 316, 322, 334, 350, 353, 354, 357, 358, 366, 377, 392, 401, 404, 411, 436, 438, 439, 443, 447, 448, 450, 451, 459, 467, 474, 491, 497, 498, 501, 502, 504, 512, 515, 516, 520, 524, 527, 528, 530, 531, 539, 544, 547, 549, 566, 573, 577, 579, 581, 599, 606, 608, 637, 643, 647, 670, 684, 686, 687, 695, 699, 700, 703, 705, 710, 717, 718, 727, 731, 735, 752, 762, 794, 801, 804, 814, 819, 822, 828, 835, 844, 853, 871, 873, 878, 884, 886, 889, 895, 898, 899, 902, 909, 915, 916, 917, 931, 936, 938, 949, 953, 968, 973, 975, 978, 995,

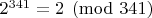
Аналогичный результат даёт и число 341: $2^{341} = 2 \pmod{341}$, т.е. ispseudoprime(341,1) как видно тоже иногда ошибается.
И таких чисел-исключений довольно много, по разным основаниям:

? for(a=2,9, print1(a,":");for(p=a+1,3000, if(!isprime(p) && lift(Mod(a,p)^p)==a, print1(" ",p))); print)
2: 341 561 645 1105 1387 1729 1905 2047 2465 2701 2821
3: 6 66 91 121 286 561 671 703 726 949 1105 1541 1729 1891 2465 2665 2701 2821
4: 6 12 15 28 66 85 91 186 276 341 435 451 532 561 645 703 946 1068 1105 1247 1271 1387 1581 1695 1729 1891 1905 2044 2046 2047 2071 2465 2701 2821 2926
5: 10 15 20 65 124 190 217 310 435 561 781 1105 1541 1729 1891 2465 2821
6: 10 15 21 30 35 105 185 190 217 231 301 430 435 481 561 777 1105 1111 1221 1261 1333 1729 1866 2121 2465 2553 2701 2821 2955
7: 14 21 25 42 105 133 231 301 325 525 561 703 817 1105 1729 1825 2101 2353 2465 2821
8: 9 14 21 28 45 56 63 65 105 117 133 153 231 273 292 341 481 511 561 585 645 651 861 949 1001 1016 1105 1106 1281 1288 1365 1387 1417 1541 1649 1661 1729 1736 1785 1905 2044 2047 2169 2465 2501 2696 2701 2821
9: 12 15 18 24 28 36 45 52 66 72 91 121 153 205 276 286 364 366 369 396 435 511 532 561 616 671 697 703 726 804 946 949 1035 1036 1105 1128 1288 1387 1541 1729 1737 1845 1854 1891 2196 2465 2501 2556 2665 2701 2806 2821 2871 2926

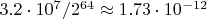
С более сильным условием сильной псевдопростоты (по основанию 2 как наиболее исследованного и применяемого в тесте BPSW) до $2^{64}$ существует 31894014 исключений (да, их можно скачать в виде 633М текстового файла, 203М в архиве). Соответственно можно грубо считать вероятность ошибки порядка $3.2\cdot10^7/2^{64}\approx1.73\cdot10^{-12}$, но она снижается с ростом чисел.
Количество таких исключений есть в A108797 и A055552.


А вот для ispseudoprime(x), выполняющей тест BPSW, исключений неизвестно. Неизвестно даже есть ли они вообще (и есть некоторые соображения что таки нет). Но прямой проверкой установлено что до $2^{64}$ их точно нет и в таких пределах она гарантированно не ошибается.
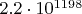
Просьба предъявить такое число, да ещё и наименьшее, смахивает на тонкое издевательство. Почти как предъявить кортеж длиной 447, нарушающий вторую гипотезу Харди-Литлвуда, которых должно быть аж 12шт до $2.2\cdot10^{1198}$, но они-то хоть точно есть, осталось только их найти ...

[EUgeneUS]

С учетом этого (болд мой):

mathpath в сообщении #1715047 писал(а):

Вероятность того, что составное число будет k раз подряд признано "вероятно простым" тестом Миллера-Рабина, строго меньше, чем (1/4)^k.

Вот это:

Yadryara в сообщении #1715049 писал(а):

Прошу рассматривать эту тему не как вопрос в ПР/Р, а как своего рода конкурс. Кто сможет предъявить такое число?

звучит как конкурс на изобретение честной монетки, которая всё время выпадает орлом.

[Yadryara]

Благодарю.

Dmitriy40 в сообщении #1715051 писал(а):

Но прямой проверкой установлено что до $2^{64}$ их точно нет и в таких пределах она гарантированно не ошибается.
Просьба предъявить такое число, да ещё и наименьшее, смахивает на тонкое издевательство.

Издевательства тут конечно нету. Я не настолько в этих вещах разбираюсь. Может как-то можно сконструировать такое число. Но интервал-то для нынешних чисел сейчас существенно больше, не $2^{64}$, а $2^{192}$.

[Dmitriy40]

Добавлю, вопрос об исключениях в тесте Миллера-Рабина активно исследовался и например нашли 7 оснований, проверка по которым не даёт исключений вплоть до как минимум $2^{64}$ (это важное число в программировании).
А ещё можно основание в тесте выбирать некоей хэш функцией от самого числа, тогда таких оснований понадобится ещё меньше.
Но насколько я понимаю вопрос об исключениях выше $2^{64}$ не исследовался.

-- 17.01.2026, 12:25 --

Yadryara в сообщении #1715055 писал(а):

Может как-то можно сконструировать такое число. Но интервал-то для нынешних чисел сейчас существенно больше, не $2^{64}$, а $2^{192}$.

Повторюсь, исключений неизвестно. И вполне вероятно (есть некие эвристические соображения) что их вообще нет.
Раз до $2^{64}$ исключений точно нет, можно очень грубо оценить вероятность как $2^{-64}\approx10^{-19}$. И с увеличением чисел она будет ещё падать. Насколько я в курсе ни мы ни вы не собирались проверять на простоту порядка $10^{20+}$ чисел, так что вероятность наткнуться на исключение невелика. А для полной уверенности можно найденные цепочки перепроверять точными тестами.

[Yadryara]

Поигрался с параметрами. Вроде понятно, что строгость возрастает при увеличении flag в ispseudoprime(x,flag). Но про flag = 0 пока непонятно. Заглянул в руководство.

https://pari.math.u-bordeaux.fr/pub/pari/manuals/2.11.1/users.pdf

185-я страница писал(а):

If flag = 0, checks whether x has no small prime divisors (up to 101 included) and is a BailliePomerance-Selfridge-Wagstaff pseudo prime. Such a pseudo prime passes a Rabin-Miller test for base 2, followed by a Lucas test for the sequence (P, 1), where P ≥ 3 is the smallest odd integer such that $P^2$ − 4 is not a square mod x. (Technically, we are using an “almost extra strong Lucas test” that checks whether Vn is ±2, without computing Un.)

Может это уже неактуально для нынешних версий.

[Dmitriy40]

Yadryara в сообщении #1715066 писал(а):

Но про flag = 0 пока непонятно.

0 эквивалентно отсутствию числа (выделение моё):

? ?ispseudoprime
ispseudoprime(x,{flag}): true(1) if x is a strong pseudoprime, false(0) if not. If flag is 0   _OR OMITTED_,   use BPSW test, otherwise use strong Rabin-Miller test for flag randomly chosen bases.

И тогда работает BPSW тест. Про него в вики есть неплохое описание.

-- 17.01.2026, 16:12 --

Yadryara в сообщении #1715066 писал(а):

https://pari.math.u-bordeaux.fr/pub/pari/manuals/2.11.1/users.pdf
Может это уже неактуально для нынешних версий.

Почему бы не посмотреть то же в актуальном (для стабильной версии 2.17.2) руководстве?
https://pari.math.u-bordeaux.fr/pub/pari/manuals/2.17.2/users.pdf

[Yadryara]

Из-за лени, видимо. Какое нашлось, в том и посмотрел. Но в новом 2.17.2 вроде написано то же самое, только на 212-й странице:

Цитата:

If flag = 0, checks whether x has no small prime divisors (up to 101 included) and is a BailliePomerance-Selfridge-Wagstaff pseudo prime. Such a pseudo prime passes a Rabin-Miller test for base 2, followed by a Lucas test for the sequence (P, 1), where P ≥ 3 is the smallest odd integer such that $P^2 - 4$ is not a square mod x. (Technically, we are using an “almost extra strong Lucas test” that checks whether Vn is ±2, without computing Un.)

[Yadryara]

Ещё не понял, зачем используется

Dmitriy40 в сообщении #1715051 писал(а):

lift(Mod(a,p)^p)

Вроде бы a^p % p даёт то же самое, только гораздо понятнее. Или в первом случае как-то взаимопростота учитывается?

Dmitriy40 в сообщении #1715056 писал(а):

Насколько я в курсе ни мы ни вы не собирались проверять на простоту

Ещё не понял какие тут "мы" и "вы".

[wrest]

Yadryara в сообщении #1715152 писал(а):

Вроде бы a^p % p даёт то же самое, только гораздо понятнее.

См. https://ru.wikipedia.org/wiki/%D0%92%D0 ... 0%BB%D1%8E

Если $p$ большое число (ну скажем больше 10 000) то $a^p$ может и не влезть в память. Ну вы же и сами можете сравнить

? for(i=1,10^5,p=random(10^5)+1;n=3^p %p)
time = 7,044 ms.
? for(i=1,10^5,p=random(10^5)+1;n=lift(Mod(3,p)^p))
time = 66 ms.
?

[Yadryara]

Спасибо.

wrest в сообщении #1715153 писал(а):

Ну вы же и сами можете сравнить

Ну так и вы и сами можете злобные смайлики не ставить

[Dmitriy40]

Yadryara в сообщении #1715152 писал(а):

Ещё не понял, зачем используется

Ради скорости.

-- 18.01.2026, 13:17 --

Yadryara в сообщении #1715152 писал(а):

Или в первом случае как-то взаимопростота учитывается?

Рази взаимной простоты используют a=2 (уж чётные p проверять малой теоремой Ферма нет нужды) или любое другое a гарантированно не делящее p (по построению p, например в поиске M48n21 с паттернами 0-3-16-2-8! все p точно не делятся на простые 2-53 из-за первой фильтрации) или проверяют делимость p на a (это быстро по сравнению с возведением в степень по модулю).