Deep associative memory

[SergeyGubanov]

SergeyGubanov в сообщении #1714583 писал(а):

$$ \vec{K}_i \to \vec{H}^{(1)}_i \to \vec{H}^{(2)}_i \to \ldots \to \vec{H}^{(N)}_i \to \vec{V}_i. $$

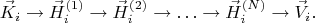
Но не существует внятного объяснения как конкретно нужно выбрать эти самые скрытые "слои".

Кажется придумал как.

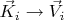
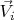
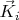
Постановка задачи. Пусть мы умеем программировать "простую" (или "не глубокую") ассоциативную память ключ-значение $\vec{K}_{i} \to \vec{V}_{i}$. Эта "простота" означает, что зависимость $\vec{V}_{i}$ от $\vec{K}_{i}$ должна быть слабо-нелинейной в том смысле, что должна требовать не очень много обучаемых параметров. Не триллион и не миллиард, а максимум несколько миллионов или даже несколько тысяч параметров. Допустим, мы хотим построить глубокую ассоциативную память (deep associative memory) из каскада простых ассоциативных воспоминаний. Например, добавив два скрытых слоя:

$$\vec{K}^{(0)}_{i} \to \vec{K}^{(1)}_{i} \to \vec{V}^{(1)}_{i} \to \vec{V}^{(0)}_{i},$$

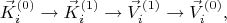
или четыре:

$$\vec{K}^{(0)}_{i} \to \vec{K}^{(1)}_{i} \to \vec{K}^{(2)}_{i} \to \vec{V}^{(2)}_{i} \to \vec{V}^{(1)}_{i} \to \vec{V}^{(0)}_{i},$$

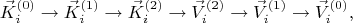
или добавив сколько угодно скрытых слоёв. Задача состоит в том, чтобы определить эти скрытые слои, отыскать принцип и написать формулы по которым эти скрытые слои можно было бы найти в явном виде.

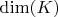
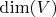
Напомню, что размерность векторного пространства ключей $\dim(K)$ и размерность векторного пространства значений $\dim(V)$ может быть разной $\dim(K) \ne \dim(V)$.

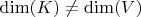
Предлагаю участникам форума рассмотреть следующее решение.

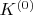
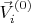
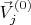
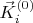
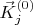
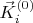
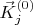
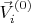
Давайте построим первый слой $K^{(1)}$ из исходных векторов $K^{(0)}$ следующим образом. Если два значения $\vec{V}^{(0)}_{i}$ и $\vec{V}^{(0)}_{j}$ соответствующие ключам $\vec{K}^{(0)}_{i}$ и $\vec{K}^{(0)}_{j}$ близки друг к другу, то мы эти два ключа $\vec{K}^{(0)}_{i}$ и $\vec{K}^{(0)}_{j}$ немного пододвинем поближе друг к другу. 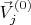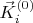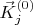А если соответствующие им значения $\vec{V}^{(0)}_{i}$ и $\vec{V}^{(0)}_{j}$ далеки друг от друга, то ключи $\vec{K}^{(0)}_{i}$ и $\vec{K}^{(0)}_{j}$ немного отодвинем подальше друг от друга. Так получим слой $K^{(1)}$, он по-построению будет слабо-нелинейно отличаться от исходного $K^{(0)}$.

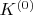
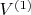
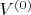
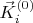
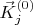
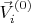
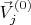
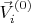
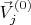
С построением первого слоя $V^{(1)}$ из исходных векторов $V^{(0)}$ всё обстоит с точностью до наоборот. Если два ключа $\vec{K}^{(0)}_{i}$ и $\vec{K}^{(0)}_{j}$ соответствующие значениям $\vec{V}^{(0)}_{i}$ и $\vec{V}^{(0)}_{j}$ близки друг к другу, то мы эти два значения $\vec{V}^{(0)}_{i}$ и $\vec{V}^{(0)}_{j}$ немного пододвинем поближе друг к другу. 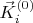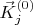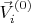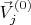А если соответствующие им ключи $\vec{K}^{(0)}_{i}$ и $\vec{K}^{(0)}_{j}$ далеки друг от друга, то значения $\vec{V}^{(0)}_{i}$ и $\vec{V}^{(0)}_{j}$ немного отодвинем подальше друг от друга. 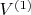Так получим слой $V^{(1)}$, он по-построению будет слабо-нелинейно отличаться от исходного $V^{(0)}$.

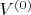
Векторы ключей движутся в ту сторону в которую им указывают двигаться соответствующие им векторы значений. А векторы значений движутся в ту сторону в которую им указывают двигаться соответствующие им векторы ключей. Повторяя эту процедуру несколько раз в конце концов получим такой слой ключей и такой слой значений, что преобразование между ними само окажется слабо-нелинейным.

Двигать ключи и значения можно, например, минимизируя следующую функцию "энергии" ($G$ - гиперпараметр, константа связи):

$$ L = \frac{1}{2} \sum_i \left( \vec{K}_{i} \right)^2 + \frac{1}{2} \sum_i \left( \vec{V}_{i} \right)^2 - \frac{G}{2} \sum_{i \ne j} \left( \vec{V}_{i} \vec{V}_{j} \right) \left( \vec{K}_{i} \vec{K}_{j} \right), $$

$$ \frac{d \vec{V}_{i} }{dt} = - \frac{\partial L}{\partial \vec{V}_{i} }, $$

$$ \frac{d \vec{K}_{i} }{dt} = - \frac{\partial L}{\partial \vec{K}_{i} }. $$

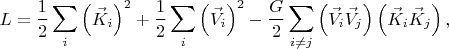
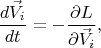
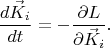
Окончательно, уравнения движения векторов $K$ и $V$:

$$ \frac{d \vec{V}_{i} }{dt} + \vec{V}_{i} = G \sum_{j \ne i} \left( \vec{K}_{i} \vec{K}_{j} \right) \vec{V}_{j}, $$

$$ \frac{d \vec{K}_{i} }{dt} + \vec{K}_{i} = G \sum_{j \ne i} \left( \vec{V}_{i} \vec{V}_{j} \right) \vec{K}_{j}. $$

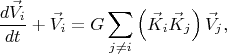
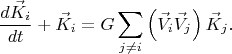
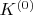
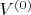
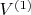
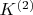
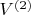
В этих уравнениях в качестве начальных значений надо взять векторы $K^{(0)}$ и $V^{(0)}$, далее численно решить эти уравнения до некоторого небольшого $t$ так чтобы векторы подвинулись, но не сильно, так получившиеся векторы и будут слоями $K^{(1)}$ и $V^{(1)}$. Интегрируя эти уравнения дальше до некоторго большего значения $t$ получим слои $K^{(2)}$ и $V^{(2)}$. И так далее, в конце концов, на некотором шаге $n$, отображение $K^{(n)}$ в $V^{(n)}$ само по себе станет слабо-нелинейным. На этом процедуру генерации слоёв можно будет остановить.

[ozheredov]

SergeyGubanov в сообщении #1715007 писал(а):

$$ \frac{d \vec{V}_{i} }{dt} + \vec{V}_{i} = G \sum_{j \ne i} \left( \vec{K}_{i} \vec{K}_{j} \right) \vec{V}_{j}, $$

$$ \frac{d \vec{K}_{i} }{dt} + \vec{K}_{i} = G \sum_{j \ne i} \left( \vec{V}_{i} \vec{V}_{j} \right) \vec{K}_{j}. $$

Там присутствуют билинейные члены от компонент векторов $K$ и $V$. Добро пожаловать в динамический хаос и не-гарантию сходимости, или я чушь несу?

[SergeyGubanov]

Ну да, неограниченный рост $K \to \infty$ и $V \to \infty$ доставит неограниченный снизу минимум $L \to -\infty$.

Надо бы как-то ограничить $L$, может так:

$$ L = \frac{1}{2} \sum_i \left( \vec{K}_{i} \right)^2 \left( \vec{V}_{i} \right)^2 - \frac{G}{2} \sum_{i \ne j} \left( \vec{V}_{i} \vec{V}_{j} \right) \left( \vec{K}_{i} \vec{K}_{j} \right), $$

$$ \frac{d \vec{V}_{i} }{dt} + \left( \vec{K}_{i} \right)^2 \vec{V}_{i} = G \sum_{j \ne i} \left( \vec{K}_{i} \vec{K}_{j} \right) \vec{V}_{j}, $$

$$ \frac{d \vec{K}_{i} }{dt} + \left( \vec{V}_{i} \right)^2 \vec{K}_{i} = G \sum_{j \ne i} \left( \vec{V}_{i} \vec{V}_{j} \right) \vec{K}_{j}. $$

[SergeyGubanov]

Хотя, если ещё раз подумать, то ведь отображение $\vec{K} \to \vec{V}$ не обязано быть обратимым, а значит двигать векторы $\vec{V}_{i}$ не надо, надо двигать только векторы $\vec{K}_{i}$ в ту сторону куда их "тянут" соответствующие им $\vec{V}_{i}$. Простейший вид функции "энергии" квадратичный по $\vec{K}_{i}$ такой:

$$ L = \frac{1}{2} \sum_i \left( \vec{K}_{i} \right)^2 - \frac{G}{2} \sum_{i \ne j} \left( \vec{V}_{i} \vec{V}_{j} \right) \left( \vec{K}_{i} \vec{K}_{j} \right), $$

Уравнения движения против градиента "энергии":

$$ \frac{d \vec{K}_{i} }{dt} + \vec{K}_{i} = G \sum_{j \ne i} \left( \vec{V}_{i} \vec{V}_{j} \right) \vec{K}_{j}. $$

Если я правильно это понимаю, то цепочка "слабых" преобразований должна бы оборваться на некотором $n$, таком что преобразование из $\vec{K}^{(n)}_{i}$ в $\vec{V}_{i}$ получается относительно "несложное":

$$\vec{K}_{i} \to \vec{K}^{(1)}_{i} \to \vec{K}^{(2)}_{i} \to \ldots \to \vec{K}^{(n-1)}_{i} \to \vec{K}^{(n)}_{i} \to \vec{V}_{i}.$$

[SergeyGubanov]

А ещё можно подтягивать скалярное произведение ключей $\langle \vec{K}_{i} \vec{K}_{j} \rangle$ к скалярному произведению соответствующих им значений $\langle \vec{V}_{i} \vec{V}_{j} \rangle$, как-то так:

$$ L = \frac{1}{4} \sum_{i} \sum_{j} \left( \langle \vec{V}_{i} \vec{V}_{j} \rangle - \langle \vec{K}_{i} \vec{K}_{j} \rangle \right)^2, $$

$$ \frac{d \vec{K}_{i}}{d t} = \sum_{j} \left( \langle \vec{V}_{i} \vec{V}_{j} \rangle - \langle \vec{K}_{i} \vec{K}_{j} \rangle \right) \vec{K}_{j}. $$

[SergeyGubanov]

Написал программку которая выравнивает скалярное произведение ключей $\langle \vec{K}_{i} \vec{K}_{j} \rangle$ к скалярному произведению соответствующих им значений $\langle \vec{V}_{i} \vec{V}_{j} \rangle$ так как описано выше. Для небольших размерностей и небольшого числа векторов оно "летает" на одном ядре, но для больших размерностей и большого числа векторов конечно простенькой программки не хватит.

После того как скалярные произведения выровнены $\langle \vec{K}^{(n)}_{i} \vec{K}^{(n)}_{j} \rangle \approx \langle \vec{V}_{i} \vec{V}_{j} \rangle$, финальное "несложное" преобразование $\vec{K}^{(n)}_{i} \to \vec{V}_{i}$ (если я всё правильно понял) является вращением в $K$-пространстве и проекцией из $K$-пространства в $V$-пространство:

$$ \vec{V}_{i} = \operatorname{const} \, {\rm Projection}\left( {\rm Rotation}\left( \vec{K}^{(n)}_{i} \right) \right). $$

[Mihaylo]

$K$ и $V$ - это, стало быть, эмбеддинги. Нужно добавить немного чего-то для связи с реальностью - входными и выходными векторами $X$ и $Y$. Энергия $L$ должна стать одним из компонентов общей функции потерь. Так ведь?

[SergeyGubanov]

В задаче ассоциативной памяти предполагается, что пары ключ-значение $\vec{K}_{i}$ и $\vec{V}_{i}$ заданы "свыше".

Как добывать $\vec{K}_{i}$ и $\vec{V}_{i}$ - это отдельная большая интересная задача.

[Mihaylo]

Попытаюсь накидать идей. Если неинтересно, то сразу скажите.

Смотрите, в процессе обучения происходит заполнение словаря (система "ключ-значение"). Ну как заполнение? Записи изначально существуют, просто они заполнены случайными значениями, и в процессе обучения они уточняются.

Очень важно, что два близких ключа должны давать примерно одинаковые значения. Это вроде как понятно? В итоге, достаточно одной записи, чтобы покрыть некоторую окрестность ключа. Интерполяция, так сказать, или генерализация, в терминах машинного обучения. Близость векторов (тензоров, эмбеддингов) определяется косинусом, если что.

Как мы заполняем и используем словарь (read, write, add, delete) - это вроде просто, но надо переложить на язык машинного обучения - должны получить дифференцируемые алгоритмы.

P.S. Я не согласен, что функция преобразования ключа в значение должна быть простой. Скорее, наоборот. Словарь тем весомее, если информация в нём сложная.