Полигармонический каскад (хотелось бы обсудить)

[Yuriy Bakhvalov]

Добрый день, уважаемые коллеги.

Я занимаюсь исследованиями на стыке теории случайных функций (Пугачев) и машинного обучения (задача регрессии). Получил несколько интересных результатов. Есть цикл статей на arXiv в cs.LG (русские версии статей есть на Preprints). Готовлю общую статью для журнала. Код всех экспериментов есть на github.

Был бы очень заинтересован в обсуждении, получении критики. Насколько “железобетонна” математика или есть нестыковки? Убедительны ли результаты экспериментов?

(надеюсь, модераторы меня не забанят, из-за того что у меня новый аккаунт, а я сразу хочу написать несколько сообщений? планирую написать ниже несколько сообщений, в каждом по отдельному моменту, чтобы не мешать в кучу)

[Ende]

Yuriy Bakhvalov в сообщении #1714411 писал(а):

надеюсь, модераторы меня не забанят, из-за того что у меня новый аккаунт, а я сразу хочу написать несколько сообщений?

Нет, не забанят.

[Yuriy Bakhvalov]

Спасибо), тогда первое о чем хотел написать:

Идея 1: вывести решение из вполне допустимых и естественных (когда нам изначально ничего не известно) симметрий вероятностной меры на пространстве функций (трансляционная, вращательная, масштабная инвариантность + гауссовость).

Результат: единственное решение: полигармонический сплайн (thin plate spline).

Но, связь полигармонических сплайнов с масштабной инвариантностью “оператора” (или алгоритма) интерполяции известна давно (например, Shaback и др.) И это дает целый класс функций ядра.

Однако, инвариантность меры на пространстве функций, это другое условие, более сильное (которое, кажется ранее не рассматривалось?). И оно указывает на единственный вариант решения, на сплайн тонкой пластины (в адаптации его в произвольной размерности).

Тогда получаем единственный вариант ядра (также, как и вся решающая схема), выведенный из первых принципов, а не взятое эмпирически.

-- 10.01.2026, 20:14 --

Полученное ядро позволяет выполнить масштабирование всей решающей схемы к работе с большими данными. Имеется обоснование, почему необходимо масштабирование вглубь и много слоёв каскада (нарушение гауссовости, когда решение вложено в пространство меньшей размерности).

В итоге получается архитектура глубокого обучения (полигармонический каскад), обучаемая не градиентным спуском (SGD) а глобальной системой линейных уравнений на каждый батч. Это похоже на метод Гаусса-Ньютона с регуляризацией Тихонова. Но примененный не к коэффициентам полигармонических уравнений (как аналоги “весов” в нейронных сетях), а в пространстве значений скрытых в слоях функций.

В итоге появляется возможность строить сверхглубокие каскады (проверено до 500 слоёв), которые продолжают работать без skip conneсtions, нормализации батчее, дропаута и т.д. Но вместо нейронов полигармонические сплайны и обучение не градиентный спуск.

-- 10.01.2026, 20:16 --

Тестировал на трех датасетах.

MNIST – результат 98.3 - 98.4 точность. По сравнению с SOTA это не много. Но в данном случае никак не учитывалось, что перед нами изображение. На вход подавался просто “мешок пикселей” (плоский вектор). При этом условии результат вполне хороший. На самом деле MNIST использовался для другого – проверить, насколько работоспособным остается алгоритм обучения, если радикальным образом менять структуру и размеры каскада (здесь и было проверено до 500 слоев).

HISSG – результат ROC AUC 0.885. На исходной выборке в 11 млн обучающих примеров (деление 10.5 млн - train, 0.5 млн - тест) а не на подвыборках как во многих тестах. Результат конкурентоспособен в сравнении с нейросетями. Единственный минус – обучение у меня получилось долгим (около 5 дней на RTX 3070). Но это первые эксперименты, и датасет не маленький все-таки.

Epsilon. Датасет отличается тем, что на входе 2 тыс. признаков. 500 тыс. примеров на train, 100 тыс. на test. Здесь наоборот полигармонический каскаж работал очень быстро. Результат ROC AUC 0.9627 (лишь чуть не дотянуло до рекорда Catboost 0.964).

[Yuriy Bakhvalov]

Обучение, кстати, часто выглядит так (для MNIST и Epsilon):

Резкий взлет на первой же эпохе.

-- 10.01.2026, 21:35 --

Ссылки:
Код на гитхабе:
https://github.com/xolod7/polyharmonic-cascade

Статьи:
English (arXiv)
Bakhvalov, Y. N. (2025). Solving a Machine Learning Regression Problem Based on the Theory of Random Functions. https://arxiv.org/abs/2512.12731
Bakhvalov, Y. N. (2025). Polyharmonic Spline Packages: Composition, Efficient Procedures for Computation and Differentiation. https://arxiv.org/abs/2512.16718
Bakhvalov, Y. N. (2025). Polyharmonic Cascade. https://arxiv.org/abs/2512.17671
Bakhvalov, Y. N. (2025). Initialization of a Polyharmonic Cascade, Launch and Testing. https://arxiv.org/abs/2512.19524

На русском (preprints.ru)
Бахвалов Ю. Н. (2024). Решение регрессионной задачи машинного обучения на основе теории случайных функций. https://doi.org/10.24108/preprints-3113020
Бахвалов Ю. Н. (2024). Пакеты полигармонических сплайнов, их объединение, эффективные процедуры вычисления и дифференцирования. https://doi.org/10.24108/preprints-3113111
Бахвалов Ю. Н. (2025). Полигармонический каскад. https://doi.org/10.24108/preprints-3113501
Бахвалов Ю. Н. (2025). Инициализация полигармонического каскада, запуск и проверка. https://doi.org/10.24108/preprints-3113659

[ozheredov]

Yuriy Bakhvalov в сообщении #1714419 писал(а):

Резкий взлет на первой же эпохе.

Для меня выглядит более удивительным, что какие-то флуктуации идут ПОСЛЕ первой эпохи (по-видимому, обусловленные стохастической природой алгоритма обучения).

Eсли взять сферический feed-forward в вакууме и заменить все функции активации на purelin - это будет чем-то принципиально отличаться от Вашего подхода?

[Yuriy Bakhvalov]

ozheredov в сообщении #1714427 писал(а):

Yuriy Bakhvalov в сообщении #1714419 писал(а):

Резкий взлет на первой же эпохе.

Для меня выглядит более удивительным, что какие-то флуктуации идут ПОСЛЕ первой эпохи (по-видимому, обусловленные стохастической природой алгоритма обучения).

Eсли взять сферический feed-forward в вакууме и заменить все функции активации на purelin - это будет чем-то принципиально отличаться от Вашего подхода?

Если увеличить, то там более подробно уже лучше видно


Нет, используется не pureline а полигармонический сплайн, который сам по себе может воспроизвести любую нелинейность. Во-вторых, полигармонический каскад, это совсем не нейросеть, где просто заменили ReLu на полигармоническое ядро. Математически он устроен иначе (например, для каждого слоя есть понятие “созвездия”, которое является основой для пакета функций, понятие, отсутствующее в обычных нейросетях). Скорее ближе к RBF. Но самое главное, процедура обучения радикально отличается. Нельзя просто реализовать его как граф вычислений, найти автоградиент по коэффициентам уравнений от ошибки и обучить Adam-ом. На каждый батч решается специальная система уравнений и затем идет синхронизированное обновление всех слоёв с учетом друг друга.

[Mihaylo]

Yuriy Bakhvalov в сообщении #1714428 писал(а):

Если увеличить, то там более подробно уже лучше видно

Я посмотрел график. Есть вероятность, что следует поиграть со скоростью обучения и прочими примочками. В вашем алгоритме есть же learning rate?

-- 11.01.2026, 05:54 --

Графики метрик можно охарактеризовать так: на первой эпохе происходит обучение, затем на последующих эпохах - застревание в локальных минимумах, "овраг" сильно изрезанный, выбраться из этих минимумов нет сил. Я бы попробовал уменьшить скорость обучения в 10/100 раз. Посмотреть, что произойдёт.
Уменьшить число гиперпараметров, упростить модель - это следующий шаг.
Какой лосс в задаче MNIST?

-- 11.01.2026, 06:00 --

Расскажите поподробнее про мешок пикселей. Ваша модель разве действительно ничего не знает про положение пикселей в изображении?

-- 11.01.2026, 06:07 --

Вы пишете в своей работе, что подаёте на вход модели изображение как 784 параметра признака - это такой упорядоченный массив (объект) или всё-таки неупорядоченный (мешок).

-- 11.01.2026, 06:17 --

Ещё могут быть не исключены прочие глупости в коде, например, неправильное вычисление метрики...

-- 11.01.2026, 06:18 --

Yuriy Bakhvalov в сообщении #1714428 писал(а):

Скорее ближе к RBF.

А как по отношению к KAN?

-- 11.01.2026, 06:45 --

Я полазил в вашем коде. Вы применяете функцию потерь $\sqrt{MSE}$. Это принципиально - извлекать корень из функции потерь MSELoss? В SGD корень не извлекается - это определяет чувствительность к ошибкам.

Показывали свой код искусственному интеллекту? Он может неплохо оптимизировать быстродействие. Надо, правда, умело с ним пообщаться.

[Yuriy Bakhvalov]

Mihaylo в сообщении #1714431 писал(а):

Yuriy Bakhvalov в сообщении #1714428 писал(а):

Если увеличить, то там более подробно уже лучше видно

Я посмотрел график. Есть вероятность, что следует поиграть со скоростью обучения и прочими примочками. В вашем алгоритме есть же learning rate?

Здесь нет настройки скорости обучения как таковой (в том смысле как понимается learning rate в НС). Есть специальный коэффициент a, который определяет насколько точно будет решена система. Хотя механизм воздействия другой, но эффект сходный с learning rate (только воздействие обратное, чем a больше, тем скорость обучения ниже, но более плавное)

-- 11.01.2026, 21:25 --

Mihaylo в сообщении #1714431 писал(а):

Графики метрик можно охарактеризовать так: на первой эпохе происходит обучение, затем на последующих эпохах - застревание в локальных минимумах, "овраг" сильно изрезанный, выбраться из этих минимумов нет сил. Я бы попробовал уменьшить скорость обучения в 10/100 раз. Посмотреть, что произойдёт.
Уменьшить число гиперпараметров, упростить модель - это следующий шаг.
Какой лосс в задаче MNIST?

-- 11.01.2026, 06:00 --

Расскажите поподробнее про мешок пикселей. Ваша модель разве действительно ничего не знает про положение пикселей в изображении?

-- 11.01.2026, 06:07 --

Вы пишете в своей работе, что подаёте на вход модели изображение как 784 параметра признака - это такой упорядоченный массив (объект) или всё-таки неупорядоченный (мешок).

Сначала про мешок пикселей. Изображение раскладывается в плоский вектор, который и подается на вход. Соответственно теряется информация о взаимном расположении пикселей. Если, например, расположение пикселей на всех изображениях из датасета перемешать случайным (но одинаковым по отношению к каждому из изображений) образом, то обучатся будет с теми же результатами.

В вики для MNIST, когда нейросеть (обычная полносвязная не сверточная) обучается именно таким образом указана ошибка 1.6% (вероятно наилучший результат). Это соответствует 98.4% точности. Это как раз та планка куда полигармонический каскад и упирается. В одном из экспериментов (описанных в 4-той статье) он стабильно достигает 98.45 – 98.5 % (если выбрать каскад с большим количеством параметров и обучать очень медленно). Т.е. это не проблема настройки обучения, а скорее потолок для самой задачи, если её поставить таким образом (плоский вектор, мешок пикселей).

-- 11.01.2026, 21:25 --

Отдельно хочу сказать, почему тест был именно такой и зачем. В целом, при проведении экспериментов не стояла цель - рекорды SOTA. Речь идет не о тюнинге известных моделей, а о потенциально другой ветви глубокого машинного обучения. И цель состояла в проведении первых экспериментов и доказательстве жизнеспособности концепции. Решалось три задачи.

1. Проверить насколько универсален предложенный алгоритм обучения (напомню, алгоритм новый, не SGD). Проверить, насколько можно менять размеры каскада, количество слоёв и т.д. Будет ли всё масштабироваться на десятки миллионов параметров и сотни слоёв?
Для этих целей и был выбран MNIST. Как известный датасет, не слишком маленький (все-таки 60 тыс. обучающих примеров и 784 входных признака), но и не слишком большой, чтобы удобно было работать на ПК.

Результат: каскад масштабируется, способен обучаться одним и тем же алгоритмом как на несколько слоёв, так и на сотни. Прямо на математике “из коробки” без какого-либо тюнинга, без skip conneсtions, нормализации батчев, без дропаута и т.д. Обучение фундаментально устойчиво.

2. Проверка работоспособности на большом зашумленном датасете со сложными нелинейными закономерностями. Для этого был выбран HIGGS.

Результаты получились вполне конкурентоспособными при сравнении с нейросетями (если ориентироваться на оригинальную статью с HIGGS). И значительно лучше таких методов как логистическая регрессия, случайны лес, бустинг деревьев.

3. Проверка работоспособности датасете с большим количеством входных признаков. Для этого был выбран тест Epsilon (у которого 2 тыс входных признаков, 500 тыс. обучающих примеров).
Здесь вообще получилось очень хорошо (особенно учитывая, что это первые эксперименты с новой архитектурой). Близко к CatBoost. (думаю, что можно было бы его превзойти если задаться такой целью). Результатов лучших чем CatBoost я в публикациях не нашел. Может быть они есть. (ИИ при вопросах к ним о результатах тестов на этом датасете начинают массово галлюционировать).

Но повторюсь, здесь цель во всех экспериментах была лишь подтвердить работоспособность концепции. И привлечь внимание к новой архитектуре.

-- 11.01.2026, 21:27 --

Mihaylo в сообщении #1714431 писал(а):

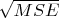
Я полазил в вашем коде. Вы применяете функцию потерь $\sqrt{MSE}$. Это принципиально - извлекать корень из функции потерь MSELoss? В SGD корень не извлекается - это определяет чувствительность к ошибкам.

Показывали свой код искусственному интеллекту? Он может неплохо оптимизировать быстродействие. Надо, правда, умело с ним пообщаться.

В коде нет функции потерь как корня из MSE. В обучении полигармонического каскада вообще не используется такое понятие как функция потерь в привычном понимании.
Но в коде действительно есть место, где вычисляется то, о чем Вы говорите, но там это лишь показатель, критерий, чтобы можно было построить графики и посмотреть, как по эпохам шёл процесс обучения. Но это в ситуации, когда решается задача регрессии. Если классификация, там вместо неё вычисляется ROC AUC.

-- 11.01.2026, 21:28 --

Mihaylo в сообщении #1714431 писал(а):

Показывали свой код искусственному интеллекту? Он может неплохо оптимизировать быстродействие. Надо, правда, умело с ним пообщаться.

ИИ код не показывал. Пока проводил тесты и писал статьи общение с ИИ на эту тему считал для себя табу (неизвестно, куда эта переписка могла бы и кому стать доступной). До тех пор, пока не появились первые препринты на preprints.ru. Но к тому времени экспериментальная часть была уже завершена (как цель, проверка концепции, результаты получились, на мой взгляд, убедительными), и актуальность в оптимизации отошла на второй план.

-- 11.01.2026, 21:30 --

Mihaylo в сообщении #1714431 писал(а):

А как по отношению к KAN?

Сравнение с KAN.

Что общего? В обоих случаях основа - это работы советских математиков 50-тых годов.

И там, и там сплайны, а также оба подхода можно рассматривать как альтернативу классическим нейросетям.

Различие.

Но в одном случае это теорема Колмогорова-Арнольда, а в другом теория случайных функций (Пугачев) + принципы индифферентности (симметрии меры).

В KAN обучаемые одномерные функции активации на ребрах (B-сплайны). В полигармоническом каскаде многомерные полигармонические сплайны (как функции ядра).

В KAN функции, это эмпирический выбор. Здесь – выводится из симметрий вероятностной меры, не выбор, а следствие.

И особенно. В KAN – обучение это градиентные спуск. Полигармонический каскад – глобальное решение линейной системы на батч (Гаусс-Ньютон подобный шаг).

[ozheredov]

Yuriy Bakhvalov в сообщении #1714484 писал(а):

Проверка работоспособности на большом зашумленном датасете со сложными нелинейными закономерностями. Для этого был выбран HIGGS.

То, что алгоритм работает на тестовых датасетах - это реально круто. Давным-давно я хотел замутить нечто похожее на RBF, но мозгов у меня, естественно, не хватило. Единственное, что вызывает опасение - не проиграет ли Ваш алгоритм вчистую конволюционкам на реальных датасетах кошечек и собачек?

[SergeyGubanov]

Yuriy Bakhvalov в Пакеты полигармонических сплайнов... писал(а):

Первая причина заключается в том, что в (2) (или в (9)) количество слагаемых равно размеру обучающей выборки. Ту же роль играет количество вершин в созвездии, если говорить о пакете. Точно также растет и количество строк и столбцов в вычисляемой обратной матрице (7) - (8), количество элементов которой (а значит и место, занимаемое в памяти) растет уже как вторая степень, а сложность вычисления как третья степень (или около неё) от этого количества.

Следовательно, если обучающая выборка начинает превышать 10-100 тысяч примеров, то решать регрессионную задачу напрямую с помощью разобранных выше выражений (1) – (7), просто наращивая количество слагаемых в (2), становится невозможным. Аналогично, использовать только один пакет полигармонических сплайнов, бесконечно наращивая количество точек в созвездии (вместо каскадного соединения нескольких пакетов) выглядит как тупиковый путь.

Постановка задачи понятна, но дальше как-то не очень...

Можно Вас попросить здесь кратко объяснить как же конкретно решается задача когда вместо одного "слоя" с числом слагаемых равному размеру обучающей выборки берётся несколько "слоёв" с числом слагаемых сильно меньше чем число примеров для обучения?

[Yuriy Bakhvalov]

ozheredov в сообщении #1714489 писал(а):

Yuriy Bakhvalov в сообщении #1714484 писал(а):

Проверка работоспособности на большом зашумленном датасете со сложными нелинейными закономерностями. Для этого был выбран HIGGS.

То, что алгоритм работает на тестовых датасетах - это реально круто. Давным-давно я хотел замутить нечто похожее на RBF, но мозгов у меня, естественно, не хватило. Единственное, что вызывает опасение - не проиграет ли Ваш алгоритм вчистую конволюционкам на реальных датасетах кошечек и собачек?

При работе с изображениями, там где работают сверточные сети, алгоритм в текущей версии конечно же им вчистую проиграет. Другое дело, что аналогично может быть создана и сверточная версия полигармонического каскада. Первые простые эксперименты, которые я проводил в этом направлении, дали отличные результаты. Но пока данное направление развивать не стал. Более актуально если прямо сейчас, то сосредоточиться на том что есть. Вижу для себя наиболее актуальное так: соединить все четыре статьи в одну, доработать её (для этого хотелось бы получить больше обратной связи от сообщества ML, других математиков) и попытаться подать в хороший журнал (хочу попытаться в JMLR). Свертки и другие модернизации вынужден пока оставить на потом, но обязательно к этому вернусь (хотя если кто-то из других математиков захотел бы попробовать в этом направлении раньше, пока я занят, то был бы этому только рад).

[Yuriy Bakhvalov]

SergeyGubanov в сообщении #1714493 писал(а):

Постановка задачи понятна, но дальше как-то не очень...

Можно Вас попросить здесь кратко объяснить как же конкретно решается задача когда вместо одного "слоя" с числом слагаемых равному размеру обучающей выборки берётся несколько "слоёв" с числом слагаемых сильно меньше чем число примеров для обучения?

Насколько понимаю, Вы сейчас смотрите вторую статью про пакеты полигармонических сплайнов, соединение их в каскад и процедуры прямого вычисления и в обратную сторону цепного дифференцирования. В этой статье решения пока еще нет, но она подводит к третьей статье "Полигармонический каскад" где уже дается алгоритм обучения. И четвертая статья, где решается последняя остающаяся задача инициализации созвездий (заодно радикально упрощая многие выражения).

Попробую ответить на Ваш вопрос. Если кратко, то думаю, что идею можно выразить так (она не так прямо выражена в статьях но по сути можно сформулировать и таким образом)... Представьте, что у нас много слоёв. И для каждого слоя у нас есть своя личная обучающая выборка. Если бы мы откуда-то заранее знали, как каждый из слоёв должен функционировать. Количество примеров для обучения в каждой из таких локальных выборок равнялось бы количеству точек в созвездиях. Или, если сказать по-другому, созвездие точек и наборы значений функций в них для этого слоя фактически и есть такая локальная обучающая выборка. Тогда мы могли бы легко создать каскад сколь угодно большой сложности и слоёв и притом каждый из них и все скрытые функции в нем сохранили бы вероятностную интерпретацию из первой статьи.

Но мы знаем только одну большую обучающую выборку с данными на входе и выходе. Мы не знаем все эти локальные обучающие выборки. Но мы можем представить, что они есть. И как раз они то и будут теми параметрами, которые мы будет итеративно шаг за шагом в процессе обучения настраивать! Ну и еще особенность, что все изменения значений во всех этих выборках (значения скрытых функций в созвездиях), во всех этих слоях мы можем завязать в одну глобальную систему уравнений и обновлять их синхронизированно на батч.

-- 12.01.2026, 02:42 --

А так получается обучение как и в нейросетях, батчами, итеративная настройка, но только это не градиентный спуск.

[Mihaylo]

Yuriy Bakhvalov в сообщении #1714484 писал(а):

Т.е. это не проблема настройки обучения, а скорее потолок для самой задачи, если её поставить таким образом (плоский вектор, мешок пикселей).

Неправильно вы, как мне кажется, применяете словосочетание "мешок пикселей". По аналогии "мешок слов" - это когда пересчитали все вхождения слов в тексте и по сути перемешали их. Flatten vector - вот это норм.

Yuriy Bakhvalov в сообщении #1714494 писал(а):

Другое дело, что аналогично может быть создана и сверточная версия полигармонического каскада.

Сверточный слой - это линейный слой с кудряво-индексным доступом к членам вектора, так что да.

[Yuriy Bakhvalov]

Mihaylo в сообщении #1714496 писал(а):

Yuriy Bakhvalov в сообщении #1714484 писал(а):

Т.е. это не проблема настройки обучения, а скорее потолок для самой задачи, если её поставить таким образом (плоский вектор, мешок пикселей).

Неправильно вы, как мне кажется, применяете словосочетание "мешок пикселей". По аналогии "мешок слов" - это когда пересчитали все вхождения слов в тексте и по сути перемешали их. Flatten vector - вот это норм.

Возможно Вы правы. Обращу внимание на формулировку.

[SergeyGubanov]

Yuriy Bakhvalov в сообщении #1714495 писал(а):

Но мы знаем только одну большую обучающую выборку с данными на входе и выходе. Мы не знаем все эти локальные обучающие выборки. Но мы можем представить, что они есть. И как раз они то и будут теми параметрами, которые мы будет итеративно шаг за шагом в процессе обучения настраивать! Ну и еще особенность, что все изменения значений во всех этих выборках (значения скрытых функций в созвездиях), во всех этих слоях мы можем завязать в одну глобальную систему уравнений и обновлять их синхронизированно на батч.

-- 12.01.2026, 02:42 --

А так получается обучение как и в нейросетях, батчами, итеративная настройка, но только это не градиентный спуск.

Можно ли расчитывать на более внятное объяснение?

В "нейронках" объяснения нет и, если, в вашем способе его тоже нет, то как бы просто поменяли шило на мыло.