Разделение переменных когда они не делятся (УЧП: Препод.)

[Red_Herring]

В курсах УЧП очень много внимания уделяется разделению переменных. Но есть случаи, когда разделить переменные можно, только если очень захочется. Начнем. с примера бигармонического уравнения $\Delta^2 u=0$. В декартовых координатах (т.е. в прямоугольнике) $u(x,y)=X(x)Y(y)$ и получаем

$$X^{IV}Y+2X''Y'' +XY^{IV} =0\implies \frac{X^{IV}}{X} + 2\frac{X''}{X}\frac{Y''}{Y}+ \frac{Y^{IV}}{Y}=0,$$

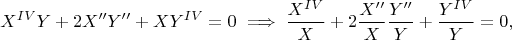
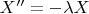
не делятся. Но можно взять $X''=-\lambda X$ потому что это уже встречалось и все хорошо: получим ОДУ для $Y$. Но нет в мире совершенства и нужны специальные граничные условия для $u$ совместимые с таким выбором, например

$$u|_{x=0}=u_{xx}|_{x=0} =u|_{x=a}=u_{xx}|_{x=a}=0,$$

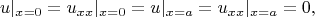
а вот

$$u|_{x=0}=u_{x}|_{x=0} =u|_{x=a}=u_{x}|_{x=a}=0$$

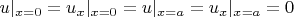
не пойдут.

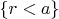
Поэтому я рассмотрю более естественный пример--то же уравнение в диске $\{r<a\}$ с условиями

$$u|_{r=a} =g(\theta), u_r|_{r=a}=h(\theta)$$

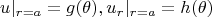
(защемленная пластинка). Тут уравнение приобретает вид

$$\left(\partial_r^2 + r^{-1}\partial_r +r^{-2}\partial_\theta^2\right)^2u=0,$$

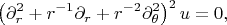
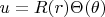
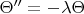
и подставляя $u=R(r)\Theta(\theta)$ просто так переменные не делятся. Но мы возьмем $\Theta''=-\lambda \Theta $ просто потому, что мы это уже видели, и с периодическими граничными условиями (диск ведь!) получаем

$$\left(\partial_r^2 + r^{-1}\partial_r -r^{-2}n^2\right)^2R=0.$$

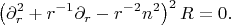
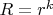
после умножения на $r^4$ получаем уравнение Эйлера и для $R=r^k$ получаем

$$((k-2)^2 -n^2)(k^2-n^2) =0.$$

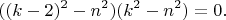
Отбрасывая сингулярные в $0$ (т.е. с отрицательными степенями $r$ или с логарифмами $r$) получаем в итоге

$$u(r,\theta)=\sum_{n=-\infty}^\infty \left(A_n r^{|n|}+B_nr^{|n|+2}\right)e^{in\theta}$$

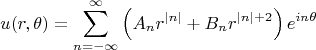
и коэффициенты находим из граничных условий.

[mihiv]

$$ \frac{X^{IV}}{X} + 2\frac{X''}{X}\frac{Y''}{Y}+ \frac{Y^{IV}}{Y}=0 \eqno (1)$$

Red_Herring
А нельзя ли обосновать выбор $X''=-\lambda X$ таким образом: дифференцируем $(1)$ по переменной $y$, а в полученном уравнении переменные уже разделяются.

[Red_Herring]

mihiv в сообщении #1714020 писал(а):

А нельзя ли обосновать выбор $X''=-\lambda X$ таким образом: дифференцируем $(1)$ по переменной $y$, а в полученном уравнении переменные уже разделяются.

Хорошее наблюдение. И наверно т о же можно проделать в полярных координатах. А можно рассмотреть "тригармоническое уравнение" и там придется дольше извращаться. Поэтому мне кажется, что лучше просто сказать "а мы это уже видели". А для систем вообще разделение переменных проблематично, н например если в линейной системе матрицы не зависят от $t$ то стоит посмотреть решения, экспоненциальные по $t$, и опять получим задачу на собственные значения (а для уравнений высших порядков м.б. пучки).

Разделение переменных это важное знание, но вытекающие из него логически ряды Фурье (и разложения по ортогональным функциям) и затем преобразование Фурье существенно важнее и более широко применяемы.