Да, существует бессконечное множество решений большинство из которых можно записать параметрически. Используя параметризацию пифагоровой тройки:
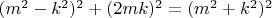
можно приравнять параметр
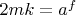
для целочисленных решений заменим
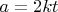
следовательно
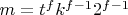
преобразуем диофантовую цепь:
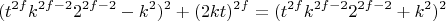
домножаем на общий параметр который хотим получить на степень
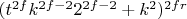
Продолжим обобщение:
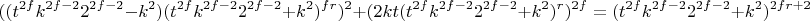
Можно также сделать обощение на коэффициенты перед степенями но смысла в этом немного, поскольку это уже полная формула для примера


Тогда наше уравнение трансформируется в такой вид
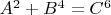
если


тогда пример:
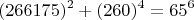
В целом видел версию с жатым уравнением Рахими ее тоже можно дополнительнить отдельно к моей параметризации. Уравнения подобные степеням

;

;
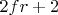
можно решить. Конкретно для вашего случая n=f ; m=fr+1 т.е. любые четные и нечетные чередования степеней n;m. Например иначе

данное уравнение неразрешимо в других вариациях (доказательства можно найти во множестве учебников). В общем основое условие разрешимости разная чётность степеней

и

. Думаю что эта параметризация является обобщенной для всех поскольку не удалено не одного слагаемого.