pan555Если я правильно понял, что Вы хотите.
Самое простое - искать инвариантное для группы симметрий уравнения решение. Но у Вашего уравнения навскидку ничего не видно, кроме сдвигов и растяжения по

. Из такой группы ничего хорошего не слепишь. Не исключено, что у уравнения есть еще какие-то неочевидные симметрии, но, чтобы их найти, надо решать определяющие уравнения.
Можно, конечно, попробовать подбирать анзатц решения наудачу.
Да, и это все про левую часть. Что там у Вас справа, я вообще не знаю.
Данная задача мне представляется аналогом уравнения Пуассона с правой частью в виде константы для центральносимметричного случая. Там решением,если я не ошибаюсь,является функция Грина.Правильно ?
Так вот,мне представляется,что и для рассматриваемого уравнения есть что то подобное.
Или я не прав ?
Р.с.
Справа у меня константа.
-- 29.12.2025, 14:09 --если и решить задачу для центральносимметрического случая
Что такое центально-симметрический случай? Если речь идет о центральной симметрии т.е.
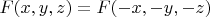
, почему бы и нет? Только решений будет очень много. А вот если речь идет о сферической симметрии, т.е. о симметрии по отношению к вращениям, то решений будет очень мало, потому что само уравнение такой симметрией не обладает. Если б у вас было бигармоническое уравнение в главной части, то задача была бы разумной.
Мне кажется, что в определенном смысле предложенное мною уравнение можно считать частным случаем бигармонического уравнения. Ну так,на первый взгляд..