Ну, как-бы да, вопросы есть. И они уже даже были сформулированы несколько раз.
Разберитесь с определениями: что такое "вычисление" и что такое "тождественное преобразование".
После этого все вопросы по этой теме должны высохнуть и отпасть.
-- 23.12.2025, 16:42 --UPD: также потребуется ознакомление с понятием "алгебраическое выражение".
Я в курсе. В частности поэтому вопросы и появились.
Это ровно то, что Вы так долго и вдохновенно оспариваете.
IMHO, ничего он не оспаривает. Это экзерсисы сложно назвать "оспариванием".
Там какая-то дикая каша. Всё смешалось: люди, кони, вычисление значения алгебраического выражения и тождественные преобразования алгебраического выражения.
А Вы, значит, любитель "какой-то дикой каши", порядочный Вы наш? Обсуждение то уж вынесли в отдельную тему, но на примитивные инсинуации то ой как тянет!...

Хотим - находим сначала значения всех функций в выражении. Хотим - сначала преобразовываем в какое угодно тождественное выражение, а потом находим значения всех функций. Хотим - находим вперемешку с тождественными преобразованиями. Ну так и где этот Ваш особый "естественный порядок" для выражений с функциями, по которому их надо находить строго на определённом этапе? :
Ну ясно же:
1. "Хотим - находим сначала значения всех функций в выражении." - это естественный порядок.
2. "Хотим - сначала преобразовываем в какое угодно тождественное выражение, а потом находим значения всех функций" - это неестественный порядок
3. "Хотим - находим вперемешку с тождественными преобразованиями. " - это - противоестественный порядок.
Никто не запрещает, но никто и не гарантирует правильность результата
Чем он неестественный-противоестественный, если получается тождественно равное выражение? Вопрос чисто риторический.
Вот простенький примерчик.
Найдите
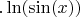
.
Никто не запрещает сначала тождественно преобразовать логарифм в функцию от икс, а затем подставить в получившееся выражение конкретное значение аргумента.
Да!.., но как эту функцию преобразовать сначала, не вычисляя синус?
-- Вт дек 23, 2025 16:52:08 --И единственный при этом известный мне "естественный порядок действий" - тот, о котором читал последний раз в учебнике максимум за 7 класс
А в учебнике за десятый класс как раз рассматривается тема "Сложная функция", где прямо сказано, что сначала вычисляется значение внутренней функции, а уже потом - значение внешней функции.
Это ровно то, что Вы так долго и вдохновенно оспариваете.
Я оспариваю целесообразность использования понятия "порядок операций" с перечислением списка из сложения, умножения, и т.д., в качестве объяснения ТС той темы её вопроса. Это типичная лишняя сущность, делающая объяснение более витиеватым, и больше ничего. Весь "порядок" заключается в следующем - "чтобы вычислить функцию от аргумента, надо сначала найти значение этого аргумента ; нельзя рассматривать аргумент отдельно от функции, в частности что-то с ним делать (складывать, умножать, и т.д. с другими компонентами выражения)". Всё это следует непосредственно из определения функции, не нужно ничего больше выдумывать. Как и не стоило долго и вдохновенно убеждать меня в целесообразности этой выдумки. Ну, это моё имхо. Объясняйте, как хотите. Только вот что-то мне подсказывает, что человек, собирающийся складывать иксы в
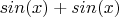
, от таких объяснений уж точно лучше предмет не поймёт...
Собственно, мне уже (давно) всё ясно. Если чего-то нового по сути вопроса добавить нечего, то все свободны.