Вот это технически непонятно. Давайте на двух примерах, вот факторизовали пару чисел:

Код:
? divisors(742798009*6)
%2 = [1, 2, 3, 6, 163, 326, 489, 978, 4557043, 9114086, 13671129, 27342258, 742798009, 1485596018, 2228394027, 4456788054]
? sqrtnint(3*742798009,3)
%3 = 1306
? select(t->t>1&&t<=%3,%2)
%4 = [2, 3, 6, 163, 326, 489, 978]
Вот только такие

и надо проверить.

подходит и даёт решение.
Код:
? 2^3*3^2*5^2*7^1*31^1*61^1*251^1/6
%1 = 996746100
? sqrtnint(3*%1,3)
%2 = 1440
? select(t->t>1&&t<=%2,divisors(6*%1))
%3 = [2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 21, 24, 25, 28, 30, 31, 35, 36, 40, 42, 45, 50, 56, 60, 61, 62, 63, 70, 72, 75, 84, 90, 93, 100, 105, 120, 122, 124, 126, 140, 150, 155, 168, 175, 180, 183, 186, 200, 210, 217, 225, 244, 248, 251, 252, 279, 280, 300, 305, 310, 315, 350, 360, 366, 372, 420, 427, 434, 450, 465, 488, 502, 504, 525, 549, 558, 600, 610, 620, 630, 651, 700, 732, 744, 753, 775, 840, 854, 868, 900, 915, 930, 1004, 1050, 1085, 1098, 1116, 1220, 1240, 1255, 1260, 1281, 1302, 1395, 1400]
Вот такие

и надо проверить.
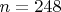
даёт решение.
-- 23.12.2025, 10:51 --Что именно делаем дальше для

Да что угодно, можно

поискать по формуле, можно разместить цепочку на место
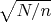
и попытаться подвинуть до суммы равной

(например как у меня выше в коде внутри первого цикла for).
-- 23.12.2025, 11:08 --Кстати, как одной командой получить вектор (сет) с элементами меньшими заданного числа?
Только что как раз применил эту команду:
nmax=sqrtnint(3*N, 3); select(t -> t>1 && t<=nmax, divisors(6*N))