Утверждение о том, что сходящаяся последовательность фундаментальна доказывается так:
1. Если последовательность сходится к

, то для любого

существует

начиная с которого разность любого элемента последовательности с

меньше

.
2. Тогда для каждого

найдётся и, например,

, начиная с которого любой элемент
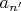
лежит в
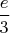
окрестности

.
3. Тогда
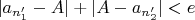
, и по неравенству треугольника
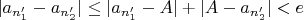
.
Я рассуждал немного иначе: если начиная с некоторого

два любых элемента находятся от

не дальше чем на

, то, кроме тривиального случая, когда эти элементы равны, есть некоторый элемент

, который ближе к

и элемент

, который дальше, но оба не дальше чем на

, то есть:
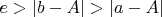
Можно ли как-то от этого прийти к
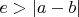
?
Можно
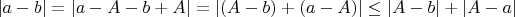
и это то что нужно, ну, кроме плюса между модулями, вместо минуса, разумеется.
Нахожу только вариант раскрыть два модуля, получив четыре решения, но что-то это не похоже на раскрытие модуля
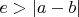
, хотя по смыслу вообще-то всё правильно:
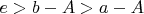
, для
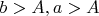
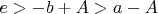
, для
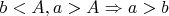
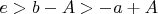
, для
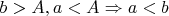
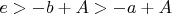
, для
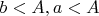
После приведения
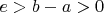
, для
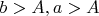
, и по условию выходит что

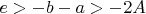
, для
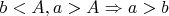
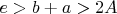
, для
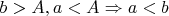

, для
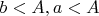
, также
