Полилинейность обратима по изначальному или всем аргументам?

[cxzbsdhwert]

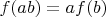
Функция $f(x)$ линейна если $f(a+b)=f(a)+f(b)$ и $f(ab)=af(b)$, и как следствие $f(ax+by)=f(ax)+f(by)=af(x)+bf(y)$

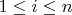
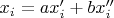
Функция $f(x_1,x_2,...,x_n)$ полилинейна, если она линейна по каждому аргументу, то есть для любого $1\leq i \leq n $, если $x_i=ax_{i}'+bx_{i}''$, то

$$f(x_1,...,ax_{i}'+bx_{i}'',...,x_n)=af(x_1,...,x_{i}',...,x_n)+bf(x_1,...,x_{i}'',...,x_n)$$

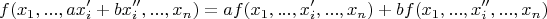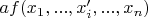
Вопрос: если в выражении $af(x_1,...,x_{i}',...,x_n)$, или аналогичном, "вернуть" вынесенный множитель $a$ в функцию, то, для выполнения равенства множитель должен умножаться только на тот аргумент, с которого он был вынесен, или на все аргументы?


Утверждение достаточно абстрактное, я пока не могу его доказать, но слышал на семинаре, что выражение линейного отображения может быть только в виде $ax$ - любые другие выражения не отображают линейно.
Тогда если $f$ полилинейна, то

$$f(x,y)=k_1x+k_2y \Rightarrow f(ax, y)=k_1(ax)+k_2y=a(k_1x)+k_2y \neq a(k_1x+k_2y) \Rightarrow f(ax,y)=af(x,y)\neq f(ax,ay)$$

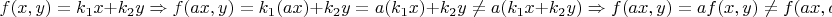
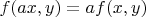
Но ведь $f(ax,y)=af(x,y)$ ложно. Как тогда? Может я не правильно представляю линейную (полилинейную) функцию по нескольким переменным?

[dgwuqtj]

Функция $k_1 x + k_2 y$ не полилинейна. Вот $f(x, y) = k x y$ полилинейна, и на её примере видно, что $a f(x, y) = f(a x, y) = f(x, a y) \neq f(a x, a y) = a^2 f(x, y)$ (последнее неравенство, разумеется, имеет исключения).

[cxzbsdhwert]

dgwuqtj в сообщении #1712778 писал(а):

Функция $k_1 x + k_2 y$ не полилинейна. Вот $f(x, y) = k x y$ полилинейна, и на её примере видно, что $a f(x, y) = f(a x, y) = f(x, a y) \neq f(a x, a y) = a^2 f(x, y)$ (последнее неравенство, разумеется, имеет исключения).

Спасибо, я это спрашиваю пытаясь разобраться с теоремой об определителе как единственной полилинейной и кососимметричной функции на множестве квадратных матриц.

Тогда получается, если рассматривать определитель как функцию от аргументов строк-векторов матрицы, то он полилинеен по этим аргументам, несмотря на то что представляет из себя сумму произведений, поскольку в каждом из слагаемых есть компонента каждого вектора, то есть каждого аргумента, и если такой аргумент, то есть вектор, скалярно умножается, то умножается каждая его компонента, и следовательно в каждой из сумм будет этот дополнительный множитель, и следовательно его можно вынести за скобки и тогда это удовлетворяет $af(x,y)=f(ax,y)=f(x,ay)$?

[dgwuqtj]

Именно так.