Доказательство делимости с помощью математической индукции

[Pavel Apuchtin]

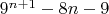
Возникла проблема вот с такой задачей: доказать с помощью математической индукции, что выражение $9^{n+1}-8n-9$ делится на 16 при $\forall n \in \mathbb{N}$. Мне удалось доказать лишь более слабое утверждение, а именно, что данное выражение делится на 8.

База индукции: при $n=1$ получаем 64. Делится и на 16, и на 8.

Теперь шаг индукции: подставим в выражение $n+1$ вместо $n$, получаем:

$9^{n+2}-8\cdot(n+1)-9=9^{n+2}-9-8n-8=9^{n+2}-9^{n+1}+9^{n+1}-9-8n-8=9^{n}\cdot81-9^{n}\cdot9+9^{n}\cdot9-9-8n-8=9^{n}\cdot(81-9)+9\cdot(9^{n}-1)-8n-8=9^{n}\cdot72+9\cdot(9^{n}-1)-8n-8$

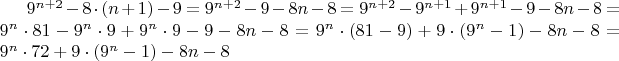
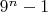
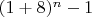
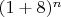
Выражение $9^{n}-1$ очевидно делится на 8 при любом натуральном $n$. Это становится понятно, если записать $(1+8)^{n}-1$ и разложить $(1+8)^{n}$ по биному Ньютона.

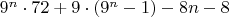
Значит, все слагаемые в выражении $9^{n}\cdot72+9\cdot(9^{n}-1)-8n-8$ делятся на 8, а значит, всё выражение целиком при любом натуральном $n$ делится на 8.


Если кому-то удастся доказать и делимость на 16, буду благодарен.

[warlock66613]

Pavel Apuchtin, обратите внимание, что у вас получилось доказательство не по индукции: вы нигде не использовали предпосылку шага индукции, что $9^{n+1}-8n-9$ делится на $16$. Попробуйте всё-таки использовать этот факт. Самым прямолинейным образом каким только возможно.

[gris]

А можно и усилить до делимости на 64

[EUgeneUS]

Pavel Apuchtin

warlock66613 в сообщении #1712541 писал(а):

Попробуйте всё-таки использовать этот факт. Самым прямолинейным образом каким только возможно.

Ещё подсказка - самым прямолинейным будет в шаге индукции добавить и отнять $9^{n+1}$.
UPD. ОМГ! Вы так и делаете. Только после этого Вас унесло не в ту степь.

gris в сообщении #1712542 писал(а):

А можно и усилить до делимости на 64

Кстати, да.

[warlock66613]

EUgeneUS в сообщении #1712563 писал(а):

самым прямолинейным будет в шаге индукции добавить и отнять $9^{n+1}$

Не, я по-другому делал. Но прицип тот же -- отнять-прибавить-сгруппировать.

[EUgeneUS]

Pavel Apuchtin в сообщении #1712521 писал(а):

Выражение $9^{n}-1$ очевидно делится на 8 при любом натуральном $n$. Это становится понятно, если записать $(1+8)^{n}-1$ и разложить $(1+8)^{n}$ по биному Ньютона.

Кстати, это становится понятно и более коротким способом:
$9^{n}-1 =(3^2)^n -1 = (3^n-1) (3^n+1)$
Произведение двух четных чисел, различающихся на $2$, обязательно делится на $8$, потому что одно из них обязательно делится на $2$, а другое на $4$.

[lel0lel]

Pavel Apuchtin
Если $9^k-8(k-1)-9\equiv 0\pmod{ 64}$, то $9^k\equiv 8k+1\pmod {64}$, и тогда $9^{k+1}-8k-9\equiv 9(8k+1)-8k-9\equiv....\pmod{ 64}$?

[Pavel Apuchtin]

Всем спасибо, всё удалось. Шаги такие:

при $n=1$ получаем 64. Делится и на 8, и на 16.

Теперь:

$9^{n+2}-9-8n-8=9^{n+2}-9^{n+1}+9^{n+1}-9-8n-8$

Понимаем, что $9^{n+1}-9-8n$ делится из-за предпосылки, остальное преобразовываем:

$9^{n+2}-9^{n+1}-8=9^{n}\cdot72-8=8\cdot(9^{n+1}-1)$

И вот здесь интересный момент: делимость числом 8 очевидна. Мы, однако, можем записать вот так:

$16\cdot\frac{9^{n+1}-1}{2}$

Поскольку $9^{n+1}-1$ делится по биному Ньтона на 8, очевидно, что $\frac{9^{n+1}-1}{2}$ - это целое число, а если мы его ещё умножили на 16, значит, получили число, делящееся на 16.

Аналогично получаем

$64\cdot\frac{9^{n+1}-1}{8}$

или

$32\cdot\frac{9^{n+1}-1}{4}$

Из этого следует делимость 64 и 32.

[Geen]

Pavel Apuchtin в сообщении #1712576 писал(а):

Шаги такие:

Всё гораздо проще: обозначим через $F_n$ вон то выражение и найдём $F_{n+1}-9F_n$...

[warlock66613]

То же самое, но с другого конца: $9^{n+2}-8(n+1)-9=9 \cdot 9^{n+1} -8(n+1)-9 = 9 \cdot (9^{n+1} - 8n-9) + \text{что-то}$