Статистическая сумма и N!

[Ascold]

Не могу понять, почему при переходе от стат. суммы для одной частицы $Z_1$ к сумме $Z$ системы неразличимых частиц во избежание суммирования(интегрирования) несколько раз по точкам фазового пространства, соответствующим перестановкам $N$ частиц, пишем

$$Z=\frac{Z_1^N}{N!},$$

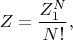
тогда как для квантовой стат. суммы будет просто

$$Z=Z_1^N?$$

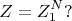
Ведь если мы поменяем местами N квантовых частицы так, что энергия системы не изменится, не будет ли это означать учёта $N!$ раз одного и того же состояния? Или дело в том, что у частиц в квантовой механике нет траектории, потому аналогия с суммированием по всем состояниям не вполне точно соответствует интегрированию по классическому пространству координат и импульсов, а состояние системы задаётся набором квантовых чисел и всё?

[Ascold]

Или я ошибаюсь и стат. сумма, скажем, N неразличимых квантовых осцилляторов тоже будет

$$Z=\frac{Z_1^N}{N!}?$$

[warlock66613]

А где вы видели неразличимые квантовые осцилляторы? Одинаковые -- да, но неразличимые?

[amon]

Ascold в сообщении #1712383 писал(а):

огда как для квантовой стат. суммы будет просто

$$Z=Z_1^N?$$

Посмотрите ЛЛ5 (статистическая физика, § 41. "Свободная энергия больцмановского идеального газа"). Если вопросы останутся - задавайте.