Материальные ур-ния для элек-ких полей через диффер. k-формы

[Divergence]

Материальные уравнения для электрических полей описываются на языке внешних дифференциальных форм

$$ {\bf D} \, = \, \varepsilon \, \star {\bf E} , $$

где $\star $- звездный оператор Ходжа, и $\varepsilon $- диэлектрическая проницаемость среды,

$$ {\bf E}\, = \, E_x({\bf x})\, dx \, + \, E_y({\bf x})\, dy \, + \, E_z({\bf x})\, dz , $$

$$ {\bf D} \, = \, D_x({\bf x})\, dy \wedge dz \, + \, D_y({\bf x})\, dz \wedge dx \, + \, D_z({\bf x})\, dx \wedge dy , $$

Подробности в статье Warnick, K.F., Russel P., Differential forms and electromagnetic field theory. Progress In Electromagnetics Research. 2014. Vol.148. P.83-112.
https://www.jpier.org/issues/volume.html?paper=14063009

Материальное уравнение ${\bf D} \, = \, \varepsilon \, \star {\bf E}$ видимо описывает только изотропный случай.

Вопрос: А как на языке дифференциальных форм, описывается анизотропный случай?
Подскажите, пожалуйста, статью или книгу где это написано на рус. или англ.
ИИ выдает ответ, но ссылок на статьи нет.

[Red_Herring]

Ссылок я тоже не знаю. То же самое, только $\varepsilon$ симметрический тензор. В Куранте "Уравнения с частными производными" есть анализ уравнений кристаллооптики

[Divergence]

Меня смущает ответ ИИ.
Для анизотропного случая ИИ утверждает, что материальные уравнение имеет вид

$$ {\bf D} \, = \, (\star \, \varepsilon) \, \wedge {\bf E} , $$

где ${\bf D}$ и ${\bf E}$ - это 2-формa и 1-форма соотвестенно, как описано выше,
и $\varepsilon$ - это 2-форма.
Значит диэлектрическая проницаемость среды должна описываться 2-формой

$$ \varepsilon \, = \, \varepsilon_{yz} ({\bf x})\, dy \wedge dz \, + \, \varepsilon_{zx}({\bf x})\, dz \wedge dx \, + \, \varepsilon_{xy}({\bf x})\, dx \wedge dy , $$

то есть антисимменричным тензором $\varepsilon_{kl}=-\varepsilon_{lk}$.

Однако, обычно диэлектрическая проницаемость среды является симметричным тензором второго ранга в анизотропных средах.

Red_Herring Спасибо за ссылку, но мне интересен именно язык дифференциальных k-форм.

[Red_Herring]

Divergence в сообщении #1711789 писал(а):

Значит диэлектрическая проницаемость среды должна описываться 2-формой

которая явно неправильна: посмотрите хотя бы случай изотропной среды, где эта формула дает 0. Т.е. либо ИИ врет, либо вы его ответ неправильно интерпретируете.

Исходите из формулы

$$ \int \varepsilon \mathbf{E}\cdot \mathbf{E} dV = \int \mathbf{D}\wedge \mathbf{E}, $$

и тогда $\mathbf{D} = \star (\varepsilon \mathbf{E})$.

[Divergence]

Спасибо за ответ.

1) Скобки я поставил. В ответе ИИ без скобок

$$ {\bf D} \, = \, \star \, \varepsilon \, \wedge {\bf E} . $$

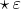
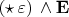
Поставил скобки, чтобы совпадали ранги дифференциальных форм: $\varepsilon$ - это 2-форма, тогда $\star \, \varepsilon$ - это 1-форма, ${\bf E}$ - это 1-форма, тогда $(\star \, \varepsilon) \, \wedge {\bf E}$ - это 2-форма, что совпадает с рангом 2-формы ${\bf D}$.

2) ИИ выдал еще и другую формулу

$$ {\bf D} \, = \, \star \, (\varepsilon \, \wedge\star {\bf E}) , $$

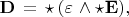
которая, по моему, не верна, поскольку не совпадение рангов дифференциальный форм (здесь скобки поставлены ИИ).

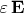
3) В вашей формуле не непонятно произведение $\varepsilon \, {\bf E}$, поскольку это дифференциальные формы 2-го и 1-го рангов.
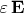
Видимо, для совпадения рангов, надо полагать, что $\varepsilon \, {\bf E}$ -это 1-форма

$$ \varepsilon \, {\bf E}\, = \, \sum^3_{j=1}\varepsilon_{ij} \,E_j({\bf x})\, dx^i . $$

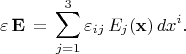
Но так почему-то не пишут.

[Red_Herring]

С какой стати $\varepsilon$ дифференциальная форма? Это симметрическая матрица. В изотропном случае она превращается в скаляр. И в любом случае $\mathbf{E}$ и $\varepsilon \mayhbf{E}$ это 1-формы.

[Divergence]

Мне тоже это не понятно, что ИИ пишет "тензоры рассматриваемые как 2 -формы".
Что бы это значило?

[Red_Herring]

Divergence в сообщении #1711873 писал(а):

Что бы это значило?

Что второе "И" это "Идиотизм"

[Divergence]

Новый вопрос к ИИ дал ответ.

"Оператор Ходжа (Hodge star operator) в анизотропных случаях обобщает свое действие, переходя от стандартной метрики к анизотропной метрике (или тензору), что меняет правила взвешивания и преобразования дифференциальных форм, сохраняя при этом свою основную роль в связывании q-форм с (n-q)-формами, но с учетом локальных «размеров» и «направлений» пространства, что важно для физических моделей, где свойства среды зависят от направления

В отличие от изотропного (Риманова) случая, где оператор Ходжа зависит только от метрического тензора и ориентации, в анизотропном случае в его определение явно входят тензоры материальных свойств среды (например, диэлектрическая и магнитная проницаемость, тензор электропроводности). "

Мне понятнее не стало.
Возможно есть пояснение в статье, но пока достать ее не могу
"Hodge duality between stress space and strain space in anisotropic media"
https://doi.org/10.1002/zamm.202100244

[warlock66613]

(Оффтоп)

Divergence в сообщении #1711876 писал(а):

но пока достать ее не могу

Есть же не совсем законные, но эффективные методы для таких случаев...

[Divergence]

Видимо диэлектрическая проницаемость среды используется ка метрический тензор и оператор Ходжа опредеяется по этой метрике

"Generalized Hodge Operator Definition: Material Tensors as Metrics: The key idea is to treat the material tensors (like the permittivity tensor as defining the inner product or "metric" for the space of differential forms.
The Hodge operator for anisotropic media is not a single fixed operator but a family of operators defined by the material's directional properties, enabling geometric descriptions of physical laws. "

warlock66613 У меня Sci-Hub не прошел, статья не достаточно старая. Запросил авторов.

[Red_Herring]

Что касается статьи, то она об анизотропной теории упругости, и там вместо 1-форм (т.е. ковекторов) симметричные 2-тензоры деформации и напряжений и вместо метрического тензора тензор упругости ранга 4, с кучей симметрий.

Я вовсе не уверен, что все это содержательная деятельность. Скорее наоборот.