kpod p pq pqr pqrs pqrst p2q p2qr p2qrs p2qrst
10^40: 10000: [ 861, 2523, 3060, 2196, 955, 1, 9, 13, 4] 1min, 59,899 ms
[ 0, 592, 1476, 1552, 824, 1, 9, 13, 4] <2^12
[ 0, 157, 288, 205, 67, 0, 0, 0, 0] <2^14
[ 0, 197, 364, 199, 42, 0, 0, 0, 0] <2^17
[ 0, 173, 246, 136, 17, 0, 0, 0, 0] <2^20
[ 0, 183, 248, 68, 5, 0, 0, 0, 0] <2^24
[ 861, 1221, 438, 36, 0, 0, 0, 0, 0] >2^24
kpod p pq pqr pqrs pqrst p2q p2qr p2qrs p2qrst
10^45: 10000: [ 729, 2329, 3080, 2266, 1092, 2, 9, 8, 7] 6min, 55,747 ms
[ 0, 513, 1431, 1555, 921, 2, 9, 8, 7] <2^12
[ 0, 132, 262, 195, 76, 0, 0, 0, 0] <2^14
[ 0, 153, 345, 229, 61, 0, 0, 0, 0] <2^17
[ 0, 117, 256, 124, 21, 0, 0, 0, 0] <2^20
[ 0, 146, 241, 101, 11, 0, 0, 0, 0] <2^24
[ 729, 1268, 545, 62, 2, 0, 0, 0, 0] >2^24
kpod p pq pqr pqrs pqrst p2q p2qr p2qrs p2qrst
10^50: 10000: [ 659, 2225, 2901, 2388, 1221, 1, 6, 10, 2] 20min, 26,544 ms
[ 0, 495, 1246, 1569, 999, 1, 6, 10, 2] <2^12
[ 0, 109, 260, 236, 102, 0, 0, 0, 0] <2^14
[ 0, 143, 339, 227, 68, 0, 0, 0, 0] <2^17
[ 0, 108, 216, 146, 26, 0, 0, 0, 0] <2^20
[ 0, 121, 229, 108, 19, 0, 0, 0, 0] <2^24
[ 659, 1249, 611, 102, 7, 0, 0, 0, 0] >2^24
kpod p pq pqr pqrs pqrst p2q p2qr p2qrs p2qrst

 таких исключений точно нет. Простые она не пропускает, но не все числа что она заявила как простые реально простые (хотя исключений и не известно). Зато если сказала составное - точно составное, без исключений.
таких исключений точно нет. Простые она не пропускает, но не все числа что она заявила как простые реально простые (хотя исключений и не известно). Зато если сказала составное - точно составное, без исключений. и
и 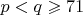 .
.


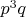

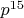
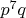

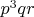

 ,
,  ,
,  ,
,  — простые числа, причём
— простые числа, причём 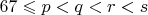 .
.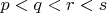 про
про