Отношения внешнего и "обычного" дифференциалов

[Yuichi196883]

На втором курсе университета, в третьем семестре мы проходили гладкие многообразия и дифференциальные формы, но при этом, нотация с первого курса (там у нас были классические дифференциалы, и высшие в том числе, обозначались через $d$) не поменялось, бывали такие ситуации, что приходилось в рамках одной задачи использовать и внешний и обычный дифференциалы, что приводило к путанице у многих студентов (у меня в том числе). Почему в современных курсах анализа на многообразиях никто не разделяет нотацию для обычного дифференциала и внешнего во избежании путаницы? Более того, часто бывает так, что обычный дифференциал интерпретируют просто как разновидность нотации, что $dx$ это просто такой значок, хотя при этом давно уже существует теория касательных пространств высшего порядка $T^pM$, которая позволяет полностью формализовать те же высшие дифференциалы (например для $f\colon M\to\mathbb{R}$ имеем $d^2f=\frac{\partial^2f}{\partial x^i\partial x^j}dx^idx^j+\frac{\partial f}{\partial x^i}d^2x^i$, при чем $d^2x^i$ не обновляются, они являются самостоятельными ковекторами второго порядка, дабы избежать путанницы, частный дифференциал можно обозначить, например, при помощи символа $D$), таким образом, можно легко избежать путаницы и неполноты картины у студента. Почему так никто не делает?

[Padawan]

Yuichi196883 в сообщении #1710649 писал(а):

при этом давно уже существует теория касательных пространств высшего порядка $T^pM$, которая позволяет полностью формализовать те же высшие дифференциалы (например для $f\colon M\to\mathbb{R}$ имеем $d^2f=\frac{\partial^2f}{\partial x^i\partial x^j}dx^idx^j+\frac{\partial f}{\partial x^i}d^2x^i$, при чем $d^2x^i$ не обновляются, они являются самостоятельными ковекторами второго порядка

Можно подробнее? Что такое $T^pM$? У меня были похожие идеи насчет $d^2f$, мне правда интересно, как формализуется второй дифференциал числовой функции на многообразии. Это элемент пространства струй (джетов) ?

-- Ср ноя 26, 2025 01:53:45 --

Yuichi196883 в сообщении #1710649 писал(а):

Почему так никто не делает?

Просветите, будем делать.

[Yuichi196883]

Касательное расслоение высшего порядка обычно вводится как расслоение струй из окрестности нуля $\mathbb{R}$ в само многообразие $M$, то-есть $T^pM = J^p_0(\mathbb{R},M)$, есть ещё вариант с многомерным пространством в основании $T^p_nM=J^p_0(\mathbb{R}^n,M)$, подробнее об этих понятиях можно почитать в работе Эресмана "C. Ehresmann Les prolongements d’une variété differentiable", в частности, $T^1$ совпадает с обычным функтором касательного расслоения. Сами эти расслоения являются векторными, базис в слое расслоения $T^pM$ задаётся (естественно, для $C^\infty$-гладких многообразий) операторами $\frac{\partial^l}{\partial x^{i_1}\dots\partial x^{i_l}}$, в сопряженном расслоении $T^{p\ast}M$ базисом будет $d^{i_1}x^{j_1}\dots d^{i_l}x^{j_l}$, $i_1+\dots+i_l = p$. Например, для случая $p=2$ будут выполняться тождества $d^2x^i(\frac{\partial}{\partial x^j}) = \delta^i_j$, $d^2x^i(\frac{\partial^2}{\partial x^j\partial x^k}) = 0$, $dx^idx^j(\frac{\partial}{\partial x^k}) = 0$, $dx^idx^j(\frac{\partial^2}{\partial x^k\partial x^l}) = \frac{1}{2}(\delta^i_k\delta^j_l+\delta^j_k\delta^i_l)$

-- 26.11.2025, 00:48 --

Сам же дифференциал функции $f\colon\mathbb{R}\to M$ задаётся как поток $s(x)=j^p_xt_{f(x)}\circ f$, где $t_{f(x)}\colon\mathbb{R}\to\mathbb{R}$ — трансляция, переводящая $f(x)$ в 0.

[dgwuqtj]

Yuichi196883 в сообщении #1710649 писал(а):

Почему в современных курсах анализа на многообразиях никто не разделяет нотацию для обычного дифференциала и внешнего во избежании путаницы?

А почему обычный дифференциал не является частным случаем внешнего? Он из функции делает 1-форму.

[Yuichi196883]

Ни внешний дифференциал, ни обычный не являются частными случаями друг друга, лба они, вообще говоря, являются частными случаями дифференциальных операторов. Под дифференциалом в первом курсе подразумевают дифференцирование, его можно применять к функции несколько раз чтоб получать высшие дифференциалы, например, второй дифференциал $d^2$, который, в этом случае, не равен нулю и является симметрическим полидифферннцированием. В свою очередь внешний дифференциал это кососимметрическое полидифферннцирование. В терминологии дифференциальных форм нельзя говорить о инфинитезимальной информации более чем первого порядка, грубо говоря нам доступна только первая производная функции, так-как вторая обновляется согласно свойствам внешнего дифференциала

-- 26.11.2025, 03:58 --

Кароче говоря, если мы берем только первый порядок, то они действительно идентичны, если же мы хотим рассматривать случаи более высокого порядка, обычный дифференциал и внешний отличаются существенно

[dgwuqtj]

У меня такое ощущение, что обычно на многообразиях высшие обычные дифференциалы не рассматривают (да, есть струи, но с ними не сильно удобно работать), а просто пишут всё в локальных координатах. То есть явно выписывают частные производные нужных порядков и проверяют независимость результата от координат при необходимости. А обозначения уже устоялись, они такие и в учебниках, и в статьях, и в монографиях.

[Yuichi196883]

Просто высшие дифференциалы нужны, например, в геометрии, бывают геометрии Картана которые нельзя достаточно хорошо описать только в первом порядке, да и, например, та же связность представляет из себя геометрическую структуру второго порядка, это можно заметить, например, по закону изменения символов Кристоффеля, по этому чисто формально второй и т. д. дифференциалы нужны, да и удобная нотация уже давно разработана для их использования.

[Padawan]

Yuichi196883
А второй дифференциал отображения многообразий $f\colon M\to N$ имеет смысл?

[Padawan]

Можно записать $df\colon TM\to TN$, где $TM$ -- касательное расслоение многообразия $M$. Тогда второй дифференциал $d(df) \colon T(TM) \to T(TN) $. Остаётся понять, как эти повторные касательные расслоения связаны с джетами, и что это будет в случае числовой функции. И как это соотносится с классическим вторым дифференциалом отображения $\mathbb R^m\to \mathbb R^n$?

[Yuichi196883]

Нет особого смысла рассматривать $d(df)\colon T(TM)\to T(TN)$, ибо $T^2M\subseteq T(TM)$, для определения вторых дифференциалов и выше используется касательный функтор высшего порядка: $T^pf\colon T^pM\to T^pN$, только их ненадо путать с дифференциалом $d^p(f)(x)=j^p_x(t_{f(x)}\circ f)$, это разные понятия. Можно так же определить всё это более общим образом при помощи алгебр Вейля и функторов Вейля, или, если и этого недостаточно, использовать определение дифференциалов из EGA 4

[VanD]

Я бы хотел уточнить конструкцию из

Yuichi196883 в сообщении #1710669 писал(а):

Сами эти расслоения являются векторными, базис в слое расслоения $T^pM$ задаётся (естественно, для $C^\infty$-гладких многообразий) операторами $\frac{\partial^l}{\partial x^{i_1}\dots\partial x^{i_l}}$, в сопряженном расслоении $T^{p\ast}M$ базисом будет $d^{i_1}x^{j_1}\dots d^{i_l}x^{j_l}$, $i_1+\dots+i_l = p$. Например, для случая $p=2$ будут выполняться тождества $d^2x^i(\frac{\partial}{\partial x^j}) = \delta^i_j$, $d^2x^i(\frac{\partial^2}{\partial x^j\partial x^k}) = 0$, $dx^idx^j(\frac{\partial}{\partial x^k}) = 0$, $dx^idx^j(\frac{\partial^2}{\partial x^k\partial x^l}) = \frac{1}{2}(\delta^i_k\delta^j_l+\delta^j_k\delta^i_l)$

Как я понимаю, имеются в виду расслоения над $M$. Пусть $m$ обозначает размерность $M$. Тогда, если я правильно понимаю обозначения, размерность слоя расслоения $J_0^2(\mathbb{R}, M)\to M$ равна $2m$ (адаптированными координатами в его слое служат $\dot{x}^i$ и $\ddot{x}^i$, $i = 1, \ldots, m$). Словам про векторность расслоения и базис из конструкции выше у меня не получается придать смысл, но ясно, что так или иначе размерность слоёв там заведомо другая. Что всё-таки имелось в виду?

[Yuichi196883]

Уточнене конструкции, касательное расслоение высшего порядка это расслоение $(T^{p*}M)^*=J^p(M,\mathbb{R})_0^*$, в этом слуае все правильно работает

[VanD]

Yuichi196883 в сообщении #1715533 писал(а):

Уточнене конструкции, касательное расслоение высшего порядка это расслоение $(T^{p*}M)^*=J^p(M,\mathbb{R})_0^*$, в этом слуае все правильно работает

Опять же, если я правильно понимаю обозначения: в общем случае расслоение $J^p(M, \mathbb{R})_0 \to M$ не векторное. Если положить $p = 2$ и заменить локальные координаты на $M$, то, вообще говоря, окажется, что вторые производные по $t$ в новых переменных выражаются (среди прочего) через слагемые, квадратичные по старым первым производным (по $t$). Что всё-таки имеется в виду под дуальным к $J^p(M, \mathbb{R})_0$ в общем случае?

[Yuichi196883]

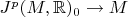
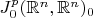
Расслоение $J^p(M,\mathbb{R})_0\to M$ как раз является векторным, просто оно ассоциированно с немного другой группой, так называемой дифференциальной группой порядка $p$, которая определяется как множество $J^p_0(\mathbb{R}^n,\mathbb{R}^n)_0$, аналогичным образом эту группу можно определить как множество автоморфизмов алгебры срезанных многочленов $\mathbb{D}^p_n=\mathbb{R}[x_1,\dots,x_n]/(x_1,\dots,x_n)^{p+1}$ в себя, эта группа является подгруппой в группе $\mathrm{GL}_N(\mathbb{R})$ 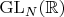для $N=\dim J^p_x(M,\mathbb{R})_0$. 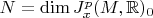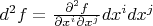Насколько я понимаю эта путанница возникает из-за неинвариантности второго дифференциала относительно смены локальной системы координат, однако тут надо понимать, что эта неинвариантность работает именно для дифференциала фреше ($d^2f=\frac{\partial^2 f}{\partial x^i\partial x^j}dx^idx^j$), однако тот дифференциал о котором мы говорим, на самом деле правильнее будет называть кокасательным функтором, так, например, $d^2f=\frac{\partial^2 f}{\partial x^i\partial x^j}dx^idx^j+\frac{\partial f}{\partial x^i}d^2x^i$, 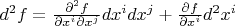и $d^2x^i$ 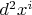являются самостоятельными векторами, они не обнуляются, в связи с чем, второй дифференциал становится инвариантным. Более общо, такого рода дифференциалы были введены ещё Гротендиком в EGA 4 и Виноградовым, только в его терминологии это были струи, а если покапаться ещё глубже, можно найти такое и в работах Эли Картана, в которых он даже указывает о бесполезности второго дифференциала в форме фреше для дифференциальной геометрии ("Теория конечных непрерывных групп и дифференциальная геометрия, изложенные методом подвижного репера" стр. 275 пункт "одновременное употребление двух систем дифференциалов", https://djvu.online/file/8e1o3zfyx0gGG), также об этом писали ещё Вэблен с Уайтхедом в основаниях дифференциальной геометрии

[VanD]

Да, я не обратил внимания на то, что там в обозначении $J^p(\ldots)$ Вы (и я следом за Вами) поменяли местами $M$ и $\mathbb{R}$. Спасибо!

В курсе анализа второй дифференциал является артефактом координатного описания, удобным для единообразной записи многочленов Тейлора, роль которых там колоссальна.
Может быть из-за этого его инвариантный аналог плохо прижился в целом. Хотя и там в случае неявного отображения $F(x) = 0$ (для векторного аргумента и функции) для нахождения вторых производных одних наборов координат по другим удобно писать $d^2 x^i$ для всех координат до последнего, чтобы в самом конце решить какие переменные независимые и так восстановить вторые производные зависимых. Это удобно чисто технически, когда нужно получить выражения для вторых производных для разных выборов независимых переменных (аналогично для старших производных). Возможность так делать является отражением того факта, что в этом случае система $F = 0, dF = 0, d^2 F = 0$ имеет в качестве решений пути (точнее, классы эквивалентности), имеющие второй порядок касания с (пусть регулярной) поверхностью $F(x) = 0$. То есть инвариантность системы связана с осмысленностью подстановок вида $dx^i = \dot{x}^i dt, d^2x^i = \ddot{x}^i dt^2$. Так понимаемый $d^2f$ в точке вычисляет ускорение изменения $f$ по 2-джету пути, описывающему движение аргумента. Но задача о старших производных при разных выборах независимых переменных, видимо, слишком частная для анализа.

Вообще у меня тоже есть ощущение какой-то недосказанности на эту тему в базовых курсах.