Излучение электрона в квантовом гармоническом осцилляторе

[fizGSE]

Предположим, у меня есть гармонический осциллятор (для простоты, одномерный). В момент времени $t=0$, я помещаю электрон в точку $x=x_0$. Моя интуиция подсказывает, что в таком случае волновая функция электрона в начальный момент времени будет чем-то вроде достаточно узкой гауссианы с максимумом в точке $x_0$ (возможно, все совсем не так, поправьте в таком случае, пожалуйста).

Такое состояние не является стационарным. Однако, в атомной физике обычно считается, что электроны в атомах находятся именно в стационарных состояниях. Мне не кажется, что потенциал моего гармонического осциллятор так уж хуже потенциальной ямы атома, так что и здесь я ожидаю от электрона схожего поведения. Следовательно, электрон должен как-то перейти из начального состояния в стационарное. Сперва я наивно предположил, что это произойдет само собой с течением времени, но, проведя расчеты, понял, что волновая функция в описанном случае периодична по времени и в волновую функцию стационарного состояния переходить не собирается. За счёт чего тогда электрон перейдет в стационарное состояние? Быть может, это будет такой же спонтанный излучательный переход, что и между стационарными состояниями, но со случайной (распределенной по некому закону) частотой?

[Alex-Yu]

fizGSE в сообщении #1710546 писал(а):

Быть может, это будет такой же спонтанный излучательный переход, что и между стационарными состояниями, но со случайной (распределенной по некому закону) частотой?

Да. Причем не один переход, а, вообще говоря, много (суперпозиция 1-го перехода, двух переходов и т.д)

[realeugene]

fizGSE в сообщении #1710546 писал(а):

Следовательно, электрон должен как-то перейти из начального состояния в стационарное.

Для этого вам нужно добавить в рассматриваемую модель как минимум электромагнитное поле с его фотонами. Без возможности излучить фотон электрон будет оставаться в суперпозиции возбуждённых состояний вечно.

[pppppppo_98]

fizGSE в сообщении #1710546 писал(а):

За счёт чего тогда электрон перейдет в стационарное состояние?

за счет взаимодействия осцилятора с ЭМ полем, которое есть всегда, но вы его выбросили из вашего рассмотрения

Alex-Yu в сообщении #1710577 писал(а):

Быть может, это будет такой же спонтанный излучательный переход, что и между стационарными состояниями, но со случайной (распределенной по некому закону) частотой?

нет....в дипольном (основном) приближении излучения разрешенные переходы гармонического осцилятора на один уровень выше и ниже, так что - наблюдаться только моночастота - идеальный лазер

[fizGSE]

Alex-Yu в сообщении #1710577 писал(а):

Да. Причем не один переход, а, вообще говоря, много (суперпозиция 1-го перехода, двух переходов и т.д)

Имеются ввиду переход с первого уровня на нулевой, со второго на первый и со второго на нулевой, и т.д.?
И в результате получится что-то вроде "фотона с различными частотами", ровно так же, как у меня в осцилляторе "электрон с различными энергиями"?

[realeugene]

fizGSE в сообщении #1710593 писал(а):

И в результате получится что-то вроде "фотона с различными частотами", ровно так же, как у меня в осцилляторе "электрон с различными энергиями"?

А как потом отличить суперпозицию различных частот фотона от статистической смеси фотонов разных частот?

[fizGSE]

realeugene в сообщении #1710601 писал(а):

А как потом отличить суперпозицию различных частот фотона от статистической смеси фотонов разных частот?

Смесь предполагает наличие нескольких частиц, а один фотон с разными частотами - это один фотон. Как по мне.

[realeugene]

fizGSE в сообщении #1710605 писал(а):

Смесь предполагает наличие нескольких частиц, а один фотон с разными частотами - это один фотон.

Нет. Смесь - это когда чистый классический теорвер, а суперпозиция - когда линейные комбинации разных состояний с комплексными весами. Смесь может быть и одного фотона разной энергии с каким-то распределением вероятности.

[epros]

Этот вопрос недавно обсуждался с моим участием. Да ещё и в связи с вопросом о том, где там могут начинать "ветвиться миры".

[realeugene]

epros в сообщении #1710609 писал(а):

Этот вопрос недавно обсуждался с моим участием.

Возможно, это один из вечных вопросов.

[Cos(x-pi/2)]

Это стандартная задача. ТС задал начальное (скажем, в нулевой момент времени ) состояние осциллятора $|\psi(0)\rangle$ как суперпозицию стационарных состояний осциллятора с заданными коэффициентами, и при этом начальное состояние ЭМ-поля как вакуумное $|0\rangle,$ т.е. ноль квантов поля. Действуем на это состояние системы "осциллятор + поле" линейным оператором её эволюции $U(t),$ в него входит гамильтониан взаимодействия осциллятора и поля.

Тем самым должен получиться вектор состояния системы к моменту времени $t,$ можно его вычислять приближённо по теории возмущений. Результат будет иметь вид суммы вкладов типа $C_{n,m}(t)\,|n\rangle\otimes|m\rangle,$ где $n$ и $m$ это номер стационарного состояния осциллятора и число квантов поля (т.е. фотонов). $|C_{n,m}(t)|^2$ есть вероятность обнаружить осциллятор на уровне $n$ и при этом $m$ квантов поля.

Если начальное состояние задать матрицей плотности, то всё аналогично; только решать надо будет уравнение эволюции не для вектора состояния системы "осциллятор + поле", а для её матрицы плотности.

[realeugene]

Cos(x-pi/2) в сообщении #1710619 писал(а):

Результат будет иметь вид суммы вкладов типа $C_{n,m}(t)\,|n\rangle\otimes|m\rangle,$

Но состояние поля описывается гораздо большим количеством параметров, чем просто число фотонов. По ним осреднили, и в результате тут у нас уже матрица плотности, а не суперпозиция?

[Cos(x-pi/2)]

Если задача об осцилляторе в трёхмерном пространстве, так что речь идёт о настоящем ЭМ-поле и о заряженной частице, способной колебаться в трёх измерениях (а не какая-нибудь игрушечная одномерная модель с игрушечным полем с невырожденным спектром частот), то $n$ и $m$ это мультииндексы.

Состояния 3-мерного осциллятора $|n\rangle$ нумеруются тремя квантовыми числами. Притом разных собственных частот у него в отсутствие специальных симметрий тоже не одна, а три. У настоящего ЭМ-поля бесконечно много мод и среди них есть вырожденные по частоте. 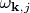Если рассматривать поле в объёме, стремящемся к бесконечности, моды можно выбрать, например, как плоские волны с частотами $\omega_{\mathbf{k},j}$ где $\mathbf{k}$ это волновой вектор, $j=1,2$ это тип поляризации. Описание состояния поля $|m\rangle$ заключается в перечислении чисел квантов $n_{\mathbf{k},j}$ в каждой моде. Т.е. мультиндекс $m$ это множество значений $n_{\mathbf{k},j}$ для бесконечного числа мод, пронумерованных волновыми векторами и номером поляризации.

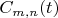
При вычислении амплитуд переходов $C_{m,n}(t)$ в пределе с $t\to\infty$ сам собой проявится закон сохранения энергии, так что останутся равными нулю числа квантов во всех модах с большими частотами - они ведь не могут возбудиться осциллятором, имеющим в начальном состоянии недостаточную для этого энергию.

В общем, такая задача похожа на недавно обсуждавшийся на форуме вопрос о вероятностях переходов, ответственных за спектральные линии спонтанного излучения атома водорода. Только тут волновые функции заряженной частицы другие, осцилляторные, а не как в кулоновском поле ядра. И начальное состояние задаётся не как одно стационарное, а как суперпозиция разных стационарных. В вычислительном плане всё будет громоздко, а в принципиальном отношении всё это не так уж и сложно.

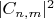
Усреднять или нет вероятности (кстати, в литературе по физике употребителен термин "усреднять", а не "осреднять") - это зависит от постановки задачи в эксперименте. Если аппаратура способна регистрировать частоты, направления волновых векторов и поляризации квантов поля, то вероятности $|C_{n,m}|^2$ для каждой моды имеют смысл отдельно друг от друга. Если же регистрируется (например, калориметром, поглощающим в итоге все кванты поля) только суммарная энергия, переданная осциллятором полю, то всё можно усреднить; правда, в такой постановке задачи заранее ясно из закона сохранения энергии, что в итоге осциллятор, перешедший в основное состояние, отдаёт полю всю свою энергию, усреднённую по его начальному состоянию, за вычетом его энергии нулевых колебаний, так что тут с полем ничего вычислять и не надо.)

[Alex-Yu]

pppppppo_98 в сообщении #1710592 писал(а):

нет....в дипольном (основном) приближении излучения разрешенные переходы гармонического осцилятора на один уровень выше и ниже, так что - наблюдаться только моночастота - идеальный лазер

Моночастота-то будет. Но переходы могут быть и не на один уровень. Не сразу, конечно, каскадно. Скажем, сперва с 10-го на 9-тый, потом с 9-го на 8-ой и т.д.

[pppppppo_98]

Alex-Yu в сообщении #1710633 писал(а):

Скажем, сперва с 10-го на 9-тый, потом с 9-го на 8-ой и т.д.

тут мы согласны
скажи серега (с)