Спектр системы связанных классических осцилляторов

[madschumacher]

Добрый день, извиняюсь за беспокойство. У меня возникла проблема, к которой я не очень понимаю как подступиться. У меня есть система из бесконечного числа связанных осцилляторов. Позиция n-го ($n\geq 0$) из них дана как $x_n$, есть собственная частота каждого осциллятора ($\omega$) и параметр связи ($\gamma$). Уравнение движение для n-го осциллятора имеет следующий вид:

$$\ddot{x}_n = -(\omega^2 - (2n+1)\gamma^2)x_n + (n+1)\gamma^2 x_{n+1} +n\gamma^2 x_{n-1} \ .$$

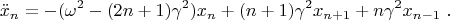
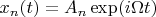
При беглом просмотре, это похоже на задачу для вывода фононов, поэтому я попытался решить это так же, подставив $x_n(t) = A_n \exp(i\Omega t)$ с амплитудой $A_n$ и собственной частотой $\Omega$, получив форму уравнения
$$-\Omega^2A_n = -(\omega^2 - (2n+1)\gamma^2)A_n + (n+1)\gamma^2 A_{n+1} +n\gamma^2 A_{n-1}$
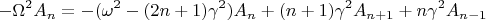
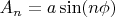
Переходя к пределу $n \gg 1$ и делая замену для амплитуд $A_n = a \sin(n\phi)$, можно получить уравнение

$$\Omega^2 = 2 n \gamma^2 (\cos(\phi)-1) + \omega^2 \ ,$$

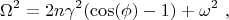
но как с ним разобраться я не очень понимаю, потому что граничных условий никаких нет.

Собственно, хотелось бы получить спектр собственных частот для такой системы, или свести её к чему-нибудь другому (например, осциллятору с трением).
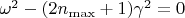
Единственная идея какая пришла, это ввести отсечку по осцилляторам $n_{\max}$, для которого частота обращается в ноль, т.е. $\omega^2 - (2n_{\max}+1)\gamma^2 = 0$, но как это можно использовать, я тоже не очень понимаю. Если будут идеи как можно подойти к этой проблеме (или идеи где можно найти её уже разобранную), буду благодарен.

[amon]

madschumacher в сообщении #1710477 писал(а):

Уравнение движение для n-го осциллятора имеет следующий вид:

$$\ddot{x} = -(\omega^2 - (2n+1)\gamma^2)x_n + (n+1)\gamma^2 x_{n+1} +n\gamma^2 x_{n-1} \ .$$

Я дико извиняюсь, но Вы при выводе этого уравнения не соврали? Для человеческих осцилляторов, вроде, должно получиться разностное уравнение с постоянными коэффициентами, а у Вас они зависят от номера осциллятора $n.$ Т.е. это либо не осцилляторы, либо где-то соврано.

[Red_Herring]

amon в сообщении #1710493 писал(а):

Для человеческих осцилляторов, вроде, должно получиться разностное уравнение с постоянными коэффициентами

если осцилляторы одинаковые

[madschumacher]

amon в сообщении #1710493 писал(а):

Я дико извиняюсь, но Вы при выводе этого уравнения не соврали?

Не соврал, к сожалению. Это не совсем честные осцилляторы, а эффективные классические осцилляторы в модели Кальдейры-Леггетта с одной внешней гармонической модой в приближении вращающейся волны, а индекс n нумерует квантовые состояния гармонического осциллятора. Именно поэтому там зависимость от степени возбуждения: чем выше возбуждение ванны, тем сильнее связь с исследуемой подсистемой. Собственно, тут идея в том, чтобы найти как внешняя ванна влияет на диссипацию возбужения в чистом состоянии для всей общей системы, без всяких внешних усреднений и прочих введений спектральных функций для ванн.

[svv]

madschumacher в сообщении #1710477 писал(а):

$$\ddot{x}_n = -(\omega^2 {\color{magenta}-} (2n+1)\gamma^2)x_n + (n+1)\gamma^2 x_{n+1} +n\gamma^2 x_{n-1}$$

А в минусе, что я выделил цветом, нет ошибки? Если бы там был плюс, правую часть можно было бы записать так:
$-\omega^2 x_n - n\gamma^2 (x_n- x_{n-1}) + (n+1)\gamma^2 (x_{n+1} -x_n)$
Два последних слагаемых тогда можно интерпретировать как силу со стороны соседних осцилляторов, как будто они связаны пружинками (причём жёсткость пружинок растёт пропорционально $n$, а минимальной потенциальной энергии пружинки соответствует нулевая длина). Каждый осциллятор тянет два соседних к себе, а они тянут его. Более того, эта сила даже удовлетворяет "третьему закону Ньютона"

[amon]

madschumacher в сообщении #1710539 писал(а):

Это не совсем честные осцилляторы, а эффективные классические осцилляторы в модели Кальдейры-Леггетта

Гамильтониан или функцию Лагранжа можете написать?

[madschumacher]

svv в сообщении #1710545 писал(а):

А в минусе, что я выделил цветом, нет ошибки?

Вроде нет ошибки, но если хотите, могу в ЛС поделиться PDFкой с выводом этого уравнения. Авось какая ещё ерунда там обнаружится...

amon в сообщении #1710595 писал(а):

Гамильтониан или функцию Лагранжа можете написать?

Да, но это не совсем напрямую из Гамильтониана выходит, а получается из уравнений эволюции волнового пакета. Опять же, могу поделиться текстом с выводом. Там, собственно, в стационарном случае у меня есть решение, но вот с временно-зависимого случая у меня не очень получается продвинуться.

[amon]

madschumacher в сообщении #1710597 писал(а):

Опять же, могу поделиться текстом с выводом.

Если можно - поделитесь, а то у Вас что-то, IMHO, странное получилось.