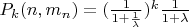Здравствуйте. Подскажите, пожалуйста, правильно ли решил задачу.
По

ячейкам размещают

частиц.
1)Найти вероятность
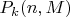
того, что в фиксированной ячейке находится ровно

частиц.
2)Найти предел
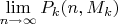
, если для последовательности


постоянно.
1)Как я понимаю, по сути это выбор с возвращением из

ячеек

раз, отсюда
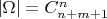
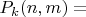

в ячейке и

в

ячейках =
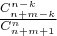
2)Для краткости тут
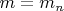
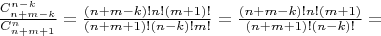
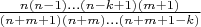

Таких будет

штука. Ещё будет один множитель
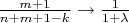
Итого