Один непонятный момент в доказательстве производной для обратной функции.
Пусть

- дифференцируемая на некотором интервале функция, для которой определена обратная

. Можно считать известным, что

и

непрерывны. По определению производной в некоторой точке
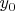
области определения

:
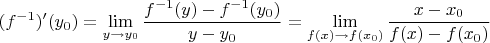
Тут, понятное дело,
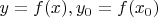
. Дальше, по идее, нужно доказать, что
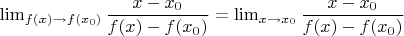
. Я доказывал так.
Пусть 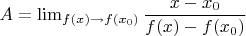 (**)
(**) . Тогда, для любого
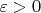
существует

, такое, что если
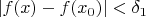
, то
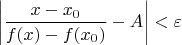
. Поскольку функция

непрерывная, то для

существует такое
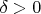
, что если

, то
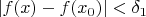
.
Объединяя два предыдущих утверждения, получим, что

.
Ну и дальше

.
Меня смущает момент, отмеченный (**). По идее, на этом этапе я уже использую то, что обратная функция дифференцируема (т.е., что этот лимит существует), что пока еще не доказано. Как это можно бы обойти? Есть вариант с доказательством через последовательности, там вроде бы такой проблемы нет. Но хотелось бы доказать через эпсилон-дельта.