Условия вывода скоростных уравнений в распределенной системе

[inevitablee]

Всем привет! Вопрос следующий. Предположим, что есть резонатор c модой $a$, и в резонаторе равномерно распределено много атомов так, что длина резонатора $ \gg \lambda $ излучения. Гамильтониан взаимодействия в приближении вращающей волны тогда выглядит так:

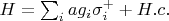
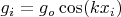
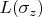
$H = \sum_i a g_i \sigma^{+}_i + H.c.$, где связь выражается через, например, $g_i = g_o \cos(kx_i) $ (стоячая волна в резонаторе) для каждого $i$-го атома. Плюс стандартные линдбладианы потерь - спонтанное излучение атомов, уширение линии перехода($L(\sigma_z)$)и потери в резонаторе.

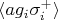
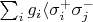
Если расписывать динамику системы, то в уравнении для $\langle a g_i \sigma^{+}_i \rangle $ появится член типа $\sum_i g_i \langle \sigma^{+}_i \sigma^{-}_j $ - корреляции между атомами. Атомы считать одинаковым нельзя, как я понимаю, поскольку они чувствуют поле в разных точках. Вопрос следующий. Описанные выше корреляции, как я понимаю, малы по величине в обычных лазерах с высокодобротными резонаторами, где основной источник потерь - атомный. Однако если речь про сверхизлучающий лазер с "плохим резонатором" (где доминируют большие оптические потери моды резонатора), то такие корреляции могут играть большую роль. Но что происходит в случае неоднородной пространственно константы связи? Интересен случай кристалла, допированного активными атомами, то есть атомов много и точно систему уравнений невозможно решить. При этом аналитически продвинуться сложно, так как вынести из суммы эффективную среднеквадратичную константу связи как будто бы нельзя, поскольку пропадет информация о фазе.

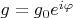
Глобально интересно, можно ли в таком случае, не прибегая к адиабатическому исключению моды резонатора, получить типичные балансные уравнения для лазера, которые будут верны, когда системы достигнет равновесия (пусть в начале уравнения будут неточными). Также если $g = g_0 e^{i\varphi}$, где$\varphi$ это азимутальный угол от $0$ до $2 \pi$, то можно ли учесть какую-то симметрию и упростить задачу? Кажется, что симметрия связи моды резонатора с атомом должна помочь.

[amon]

inevitablee в сообщении #1710054 писал(а):

$H = \sum_i a g_i \sigma^{+}_i + H.c.$, где связь выражается через, например, $g_i = g_o \cos(kx_i) $ (стоячая волна в резонаторе) для каждого $i$-го атома. Плюс стандартные линдбладианы потерь - спонтанное излучение атомов, уширение линии перехода($L(\sigma_z)$)и потери в резонаторе.

Если расписывать динамику системы, то в уравнении для $\langle a g_i \sigma^{+}_i \rangle $ появится член типа $\sum_i g_i \langle \sigma^{+}_i \sigma^{-}_j $ - корреляции между атомами.

Для начала не худо было бы уточнить какую задачу мы решаем. Лазер, как любая автоколебательная система, штука нелинейная, и линейным гамильтонианом тут не отделаться. На тему динамики лазеров написаны тома, и прежде чем отправлять Вас их читать хотелось бы понять что за задачу Вы решаете.