Ура, я выполз из-под нагромождения работы, выдохнул и временно обрел способность худо-бедно соображать. Пользуясь случаем, возвращаюсь к своим задачам.
Спасибо всем ответившим. Я разобрался с понятием условной независимости. Понятие любопытное, но, если вдуматься, очень естественное. Возьмем вероятностное пространство

. Зафиксируем событие
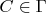
такое, что
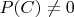
. Для каждого

определим условную вероятность
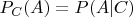
. Тогда тройка

есть новое вероятностное пространство. Условная независимость событий

относительно

в вероятностном пространстве

- это в точности независимость событий

в вероятностном пространстве

.
Думаю, условие единственности связи равносильно одновременному выполнению четырех условий:
1)

2)
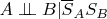
3)
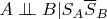
4)
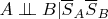
Обозначим эту четверку условий (*).
Смысл условий (*): как только ситуация с премиями определилась, события

становятся независимыми. Математически точнее - ситуация с премиями имеет четыре возможных исхода, каждый из который соответствует своему вероятностному пространству:
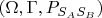
и т.д. В каждом из этих пространств события

независимы.
Вам нужно, видимо, что-то вроде
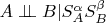
для
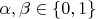
.
Хм. Не уверен, что это равносильно условиям (*). Нужно учитывать, что события

могут быть независимыми относительно

, но зависимыми относительно
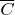
. Пример есть в википедии в статье про условную независимость, я так удивился этому факту, что тщательно его проверил. Хотя, если вдуматься, ничего удивительного нет.
(Бытовой пример)
Бытовой пример, как события

и

могут быть условно независимы относительно

, но условно зависимы относительно

. Пусть приятели Саша и Паша собираются сегодня вместе на концерт.

- "Саша сегодня с кем-нибудь пообщается",

- "Паша сегодня с кем-нибудь пообщается",

- концерт отменен. Если концерт отменен, то Саша и Паша проводят вечер порознь, и каждый сам решает, общаться ему с кем-то или нет. Если концерт не отменен, то вероятность Саши с кем-то пообщаться зависит от того, придет ли на концерт Паша. Если придет, приятели наверняка пообщаются друг с другом, а если не придет, то еще вопрос, станет ли Саша на концерте заводить знакомства.
Интуиция подсказывает, что это условие формализуется в виде
![$$
P[(A, B)|(S_A, S_B)] = P(A|S_A) P(B|S_B) \eqno{(1)}
$$ $$
P[(A, B)|(S_A, S_B)] = P(A|S_A) P(B|S_B) \eqno{(1)}
$$](https://dxdy-03.korotkov.co.uk/f/e/e/c/eece019b19bf2a62ab3538dabc3610c982.png)
А почему не:
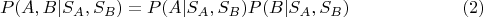

Во всяком случае, (2) - это условная независимость, а что такое (1) я не понимаю.
На самом деле я немного "гнал под ответ", как это называли в мои школьные годы. Все эти изыскания в трех соснах выросли из темы
«Неравенство Белла», где я пытаюсь разобраться с выводом неравенства Белла в теории со скрытыми параметрами, приведенном в учебнике Львовского. Автор пропускает некоторые промежуточные выкладки. В попытке их восстановить я предположил, что Львовский формализовал условие единственности связи как уравнение (1) (в этом
сообщении оно обозначено (Bell.3)). По крайней мере, если принять это уравнение, то дальнейшие выкладки сходятся, и моя слабенькая в вопросах теорвера интуиция говорила мне что-то похожее на уравнение (1).
Теперь я думаю, что условие единственности связи правильнее формализовать как (*). Я подумаю, можно ли вывести (1) из (*), а если нет, то как быть с выкладками Львовского.