Решаема ли оптимизационная задача?

[Zahar Kartashov]

Решаема ли вот такая задача?
$\min\limits_{x}\max\limits_{i\in \left\lbrace 1, \dots, N\right\rbrace}\frac{x^T Q_i x}{b_i^T x};\qquad x\in\boldsymbol{R^n}$
Тут $Q_i$ - положительно определённые матрицы. Т.е. в числителе - квадратичные формы, в знаменателе - линейные функции.

[ozheredov]

Zahar Kartashov
Ух ты ж, как красиво! А откуда возникла задача, если не секрет?

[Zahar Kartashov]

ozheredov

В числителе находятся дисперсии сигнального отклика при i-м значении параметра, в знаменателе - матожидания этого отклика. Нужно улучшить наихудший отклик.

[Alex Krylov]

Zahar Kartashov

Простите, но что-то у вас здесь не то! Ибо $\frac{x^2}{x}=x$ и это функция неограниченная!

[dsge]

Zahar Kartashov в сообщении #1709510 писал(а):

Решаема ли вот такая задача?
$\min\limits_{x}\max\limits_{i\in \left\lbrace 1, \dots, N\right\rbrace}\frac{x^T Q_i x}{b_i^T x};\qquad x\in\boldsymbol{R^n}$
Тут $Q_i$ - положительно определённые матрицы. Т.е. в числителе - квадратичные формы, в знаменателе - линейные функции.

1. Эпиграф функции $\frac{x^T Q_i x}{b_i^T x}$ выпуклое множество, значит такая функция выпуклая.
2. Функция
$\max\limits_{i\in \left\lbrace 1, \dots, N\right\rbrace}(f_1(x), \dots, f_N(x) )$
выпуклая, если $f_i(x)$ выпуклые. Значит задача выпуклая и имеет решение.
(Ограниченность функций снизу тоже надо доказать).

[Евгений Машеров]

Я бы перевернул дробь (поменяв минимумы и максимумы местами) и перепараметризовал бы $z=Q^{1/2}x$, $x=Q^{-1/2}z$

[Null]

Евгений Машеров, переворот незаконен, функция $\frac{1}{x}$ не монотонна на $\mathbb{R}$, $Q$ тоже разные.

[Евгений Машеров]

С поворотом проще, имеет смысл рассматривать только положительные значения $b_i^Tx$, для чего можно и знак при b сменить. А вот разные $Q_i$ да, проблема...

[Alex Krylov]

Цитата:

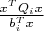
Эпиграф функции $\frac{x^T Q_i x}{b_i^T x}$ выпуклое множество

Если прям для простейшего двумерного случая посчитать матрицу Гессе для функции:
$\frac{x^T Q x}{b^T x}$
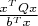
то получится, что эта функция выпуклы при условии $b^T x>0$.

Т.е. говорить, что "max{} выпуклых функций снова выпуклая функция" мы можем только при выполнении условий:
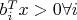
$b_i^T x>0 \forall i$. И это должно быть непустое множество!

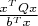
Теперь разберемся с минимумом $\frac{x^T Q x}{b^T x}$ при условиии $b^T x>0$:
$\frac{x^T Q x}{b^T x} = \frac{(C_Q^T x)^T (C_Q^T x)}{b^T x}=\frac{\left\lVert y \right\rVert^2}{(C_Q^{-1}b)^T y}$

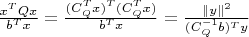
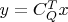
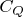
где $y=C_Q^T x$ ($C_Q$- фактор Холецкого матрицы $Q$).

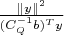
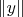
Минимум дроби $\frac{\left\lVert y \right\rVert^2}{(C_Q^{-1}b)^T y}$ при фиксированной норме $\left\lVert y \right\rVert$ достигается при $y = \alpha \frac{C_Q^{-1}b}{\left\lVert C_Q^{-1}b \right\rVert}, \alpha>0 $
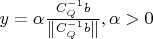
И этот минимум равен:
$\frac{\left\lVert \alpha \frac{C_Q^{-1}b}{\left\lVert C_Q^{-1}b \right\rVert} \right\rVert^2}{(C_Q^{-1}b, \alpha \frac{C_Q^{-1}b}{\left\lVert C_Q^{-1}b \right\rVert})} = \frac{\alpha^2}{\alpha \left\lVert C_Q^{-1}b \right\rVert}= \frac{\alpha}{\left\lVert C_Q^{-1}b \right\rVert}$

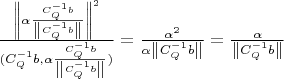
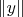
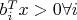
Но $\alpha$, т.е. норма $\left\lVert y \right\rVert$ у нас не ограничена. Т.е. минимума нет! Чтобы он был, нужна компактная область оптимизации. Условия $b_i^T x>0 \forall i$ могут дать пустое множество, но компактной области не дают.

[dsge]

Да, $b^T x>0$ необязанно выполняться. Если не накладывать дополнительных ограничений, то всегда можно выбрать последовательность, для которой целевая функция будет стремиться к $ - \infty$, если пересечение $\left\lbrace x: b_i^T x<0\right\rbrace, i=1,2, \dots$ непусто.

[Alex Krylov]

Цитата:

Но $\alpha$, т.е. норма $\left\lVert y \right\rVert$ у нас не ограничена. Т.е. минимума нет!

Что-то я зарапортовался, странным образом, говоря о минимуме, но отыскивая при этом максимум.

[Alex Krylov]

Минимум на множестве $b^T x>0$ отсутствует. Можно говорить лишь об инфимуме.

[Zahar Kartashov]

Спасибо участникам форума за комментарии, буду думать. Я сначала хотел решать что-то наподобие вот этого
$\min\limits_{x}\max\limits_{i\in \left\lbrace 1, \dots, N\right\rbrace}\frac{x^T Q_i x}{x^T (b_i b_i^T) x};\qquad x\in\boldsymbol{R^n}$

Но вроде как здесь совсем все плохо. Поэтому, как паллиативная мера, сформулировал задачу в том виде, как описано в заглавном сообщении. А теперь вижу, что и тут есть проблемы.

[Евгений Машеров]

Мне кажется, Ваша "изначальная" постановка выглядит перспективнее той, что в первом постинге.
Мне представляется некий эмпирический алгоритм. Находим оптимальные иксы для каждого i (кажется, тут решение может быть аналитическое) и подставляем каждое "оптимальное" в выражения для прочих i, Находим минимаксное. Затем пытаемся улучшить решение, строя линейные комбинации этого решения с решением, оптимальным для "наихудшего" для данного i.

[Zahar Kartashov]

Пока по методике из статьи *) попробовал вот такую задачу решить:
$\max\limits_{x} \sum\limits_{i=1}^{N} \frac{x^T (b_i b_i^T) x}{ x^T Q_i x};\qquad x\in\boldsymbol{R^n}$
вместо вот этой:
$\min\limits_{x}\max\limits_{i\in \left\lbrace 1, \dots, N\right\rbrace}\frac{x^T Q_i x}{x^T (b_i b_i^T) x};\qquad x\in\boldsymbol{R^n}$

На удивление работает. Причем, не только при инициализации итерационного алгоритма из статьи "хорошими решениями", известными из теории обработки сигналов, но и совершенно случайными векторами.

*) Kiers, H.A.L. Maximization of sums of quotients of quadratic forms and some generalizations. Psychometrika 60, 221–245 (1995). https://doi.org/10.1007/BF02301414