О перцептроне Розенблатта

[mihaild]

tac в сообщении #1707898 писал(а):

mihaild в сообщении #1707897 писал(а):

пороги для А-элементов

в нашем случае они равны нулю, поэтому можем от них избавится.

На всякий случай - у нас $W_{sa}$ бинарная?

[tac]

mihaild в сообщении #1708233 писал(а):

И утверждается, что при таких ограничениях алгоритм "не переобучается" (видимо, с высокой вероятностью относительно матрицы $W_{sa}$) на "разумных" датасетах?

да, но теперь нужно вернутся к понятию переобучения, по классике в нем нет понятия стабильности/отклонения , о котором я ранее говорил

-- Пн ноя 03, 2025 20:33:02 --

mihaild в сообщении #1708235 писал(а):

На всякий случай - у нас $W_{sa}$ бинарная?

со значениями +1 и -1, отсутствие связи = 0 , поэтому как посмотреть )

[mihaild]

tac в сообщении #1708236 писал(а):

со значениями +1 и -1, отсутствие связи = 0 , поэтому как посмотреть

Бинарная - это с элементами $0, 1$, так что нет.

tac в сообщении #1708236 писал(а):

да, но теперь нужно вернутся к понятию переобучения, по классике в нем нет понятия стабильности/отклонения , о котором я ранее говорил

Хорошо, теперь, когда у нас есть нормальное описание модели, можно вернуться к тому, какими магическими свойствами она должна обладать.
Мне, на самом деле, даже не очевидно, что при алгоритме генерации $W_{sa}$ выше система будет с большой вероятностью разрешима. Но в целом готов пока поверить.

[tac]

mihaild в сообщении #1708230 писал(а):

Если у нас в данных уже есть легко извлекаемый таргет, то это же хорошо.
Но я про то, что ограничение "тестовая выборка не содержит полностью отличающихся от обучающей стимулов" ничего содержательно не ограничивает, поэтому вряд ли можно что-то сказать про выборку с этим ограничением, чего нельзя сказать без него.

Если есть - то это просто банально, ок, это не на что не повлияет. А вот про вторую часть не согласен. Она убирает совершенно не релевантные примеры, которым перцептрону не было и шанса научится. Именно в этом случай возникают ваши эффекты "разгула случайности", которые вы наблюдаете как переобучение, а я мерю меру стабильности ответа. Но это мы уже обсуждали.

-- Пн ноя 03, 2025 20:45:00 --

mihaild в сообщении #1708237 писал(а):

при алгоритме генерации $W_{sa}$ выше система будет с большой вероятностью разрешима.

я на самом деле, использую другой алгоритм чаще, а не классический, он лучше ...

Алгоритм 1: Двухфазная инициализация связей
Вход: SCount = n
Выход: Матрица весов WeightSA
для каждого А-элемента a:
    для j = 1 до 2n:
        сенсор s ← случайный(1, n)
        если j ≤ n:
            вес ← 1  // возбуждающая фаза
        иначе:
            вес ← -1 // тормозящая фаза
        WeightSA[s][a] ← вес

-- Пн ноя 03, 2025 20:47:31 --

mihaild в сообщении #1708237 писал(а):

когда у нас есть нормальное описание модели, можно вернуться к тому, какими магическими свойствами она должна обладать.

ну давайте назовем это свойство - компенсатором шума.

-- Пн ноя 03, 2025 20:58:38 --

На вопрос, почему так происходит в перцептроне, я собственно никогда не задумывался, потому что как правило я не думал, что все так печально с другими алгоритмами. И несмотря на то, что вы говорите, что дело не в алгоритмах, а в частных случаях задач (обучающих выборках в связи с тестовой), я не готов с этим согласится. Очевидно, что если понятие "переобучения" появилось в связи с массовым применением бэкпропа и под него собственно и делалось, то причина его наличия наоборот в алгоритме бэкпропа - градиентном спуске.

В перцептроне, же происходят "локальные разрывы" в каждом нейроне из за пороговой функции, и причину "естественного компенсатора шума" нужно искать в этом.

-- Пн ноя 03, 2025 21:07:55 --

Я понимаю, что вы не очень любите читать выводы LLM, но его гипотезы, ниже думаю имеет смысл рассмотреть, как минимум мы поймем за счет чего это может происходить:

Цитата:

1. Распределённое кодирование и избыточность [к классическому перцептрону не относится]

# Шум легко "ломает" редкие активации
[0, 0, 1, 0, 0, -1, 0, 0] + шум → [0, 0, 0, 0, 0, -1, 0, 0] # потеря информации!

# Шум равномерно "размазывается" по многим признакам
[0.3, -0.2, 0.8, -0.1, 0.4, -0.6, 0.1, -0.3] + шум →
[0.4, -0.1, 0.9, 0.0, 0.5, -0.5, 0.2, -0.2] # структура сохраняется!

2. Компенсация ошибок через множество слабых признаков [самое простое объяснение]

* Каждый нейрон получает вклад от многих сенсоров
* Ошибка в одном сенсоре компенсируется корректными сигналами от других
* Шум имеет нулевое математическое ожидание → в среднем компенсируется

4. Статистические свойства матрицы весов [тут я мало что понял, но может поймете вы]
Алгоритм создаёт веса с:
* Нулевым средним: E[W] = 0
* Умеренной дисперсией: Var[W] ≈ 2

Это означает, что случайный шум не резонирует с структурой весов

[mihaild]

tac в сообщении #1708238 писал(а):

Она убирает совершенно не релевантные примеры, которым перцептрону не было и шанса научится

Проблема в том, что она не гарантирует их убирание. Поэтому добавление этого условия вряд ли позволит сказать что-то интересное.

tac в сообщении #1708238 писал(а):

я на самом деле, использую другой алгоритм чаще, а не классический, он лучше

Если я правильно понимаю, то этот алгоритм примерно $\left(1 - \frac{1}{e}\right) \approx 0.63$ весов инициализирует $-1$, и $\frac{1}{e} \cdot \left(1 - \frac{1}{e}\right) \approx 0.23$ инициализирует $1$. И вроде бы получается, что если у нас $n$ большое, и почти все входные координаты единичные (скажем у каждого примера 90% координат равны $1$), то с высокой вероятностью выход А-слоя будет просто нулевым на всех примерах...

tac в сообщении #1708238 писал(а):

ну давайте назовем это свойство - компенсатором шума

Про это есть хорошая народная поговорка. В чём это свойство заключается?
И какие ограничения на датасет наложены? Отсутствие противоречивых примеров и "полностью отличных" я понял, но этого недостаточно.

-- 03.11.2025, 19:55 --

tac в сообщении #1708238 писал(а):

Очевидно, что если понятие "переобучения" появилось в связи с массовым применением бэкпропа

Очевидно, что это неправда. Например, в довольно древней (1997 год) книге Митчелла, хотя back propagation и есть, но понятие переобучения рассматривается, в первую очередь, для решающих деревьев.
Там, кстати, близкое к тому, что я написал по памяти, определение.

Цитата:

Given a hypothesis space $H$, a hypothesis $h \in H$ is said to overfit the training data if there exists some alternative hypothesis $h' \in H$, such that $h$ has smaller error than $h'$ over the training examples, but $h'$ has a smaller error than $h$ over the entire distribution of instances.

tac в сообщении #1708238 писал(а):

но его гипотезы, ниже думаю имеет смысл рассмотреть

Нет, не имеет. Там какое-то рукомашество.
А ключевой вопрос - что Вы понимаете под "компенсатором шума".

-- 03.11.2025, 20:00 --

tac в сообщении #1708238 писал(а):

И несмотря на то, что вы говорите, что дело не в алгоритмах, а в частных случаях задач (обучающих выборках в связи с тестовой), я не готов с этим согласится

А с тем, что $2+2=4$, Вы согласиться готовы?

[tac]

mihaild в сообщении #1708242 писал(а):

этот алгоритм примерно $\left(1 - \frac{1}{e}\right) \approx 0.63$ весов инициализирует $-1$, и $\frac{1}{e} \cdot \left(1 - \frac{1}{e}\right) \approx 0.23$ инициализирует $1$.

Да, это так.

mihaild в сообщении #1708242 писал(а):

если у нас $n$ большое, и почти все входные координаты единичные (скажем у каждого примера 90% координат равны $1$), то с высокой вероятностью выход А-слоя будет просто нулевым на всех примерах

Это снова, искусственный вырожденный пример. И нет, это лишь означает высокий фокус, т.е. это будет означать ровно то, что и инвертированное изображение будет такое же как и число с небольшим числом признаков. Если при этом вы добьетесь что каждый стимул будет отличаться, то все в порядке. Попробуйте добиться хотя бы одного полностью нулевого выхода на А-элементах.

-- Пн ноя 03, 2025 22:40:48 --

mihaild в сообщении #1708242 писал(а):

довольно древней (1997 год)

это новая книга )) понятие переобучения для бэкпропа уже было, ну и потом никто не спорит - что это пришло на зарее становления т.н. машинного обучения, когда статистисты влезли не в свою область

-- Пн ноя 03, 2025 22:43:32 --

mihaild в сообщении #1708242 писал(а):

Нет, не имеет. Там какое-то рукомашество.
А ключевой вопрос - что Вы понимаете под "компенсатором шума".

Если не имеет, то остановимся на том, что это феномен. И только когда, вы признаете феномен, будет иметь смысл искать его причины.

-- Пн ноя 03, 2025 22:56:21 --

mihaild в сообщении #1708242 писал(а):

А с тем, что $2+2=4$, Вы согласиться готовы?

я согласится готов с тем, что возникает на практике, а не в умозрительных "мысленных экспериментах".

-- Пн ноя 03, 2025 23:23:52 --

Давайте пойдем от обратного. Если полностью обученный перцептрон (с 0 ошибкой на обучающей выборке), на тестовой выборке дает ошибку прогнозирования E $\pm$ de, выше, чем avg (En) , где n - итерация на которой было остановлено обучение, а avg (En) средние ошибок, после n, то он переобучен.

P.S. до конца в правильности формулировки не уверен, но думаю уже близко ))

[tac]

Вот пример, синия линия - это ошибка E (по y) на тестовой выборке, каждый шаг обучения (по x). Рыжая линия средние AVG(E) за на отрезке [n, N], где n -текущий шаг, а N - шаг конца обучения.

Как видим, несмотря на то, что на итерации 17 - есть ошибка = 1235, это не является переобучением, при Eend = 1255 , т.к. это не стабильное отклонение во время обучения, а средние в целом не скакнуло ниже Eend.

Неформально, я уже объяснял и мы видим очередной случай когда вначале много всплесков, но постепенно перцептрон приходит к стабильно низкой ошибке прогноза.

-- Пн ноя 03, 2025 23:45:19 --

Это кстати, результат обучения перцептрона на MNIST Fashion

[mihaild]

tac в сообщении #1708244 писал(а):

Это снова, искусственный вырожденный пример

Огласите весь список критериев "вырожденности", пожалуйста.

tac в сообщении #1708244 писал(а):

Попробуйте добиться хотя бы одного полностью нулевого выхода на А-элементах.

Возьмите любое $n > 100$, сгенерируйте $W_{sa}$ Вашим методом, сгенерируйте $\vec x_i$ бинарные, с $n$ координатами, каждая равна $1$ с вероятностью 90% и $0$ с вероятностью 10%, и возьмите тождественную функцию в качестве $S$. С гигантской вероятностью все $\vec x_i$ получатся разными, а все элементы $\vec x \cdot W_{sa}$ - неположительными.

tac в сообщении #1708244 писал(а):

понятие переобучения для бэкпропа уже было

Не то чтобы история вопроса была важной, но всё-таки хотелось бы увидеть хоть какие-то подтверждения, что

tac в сообщении #1708238 писал(а):

понятие "переобучения" появилось в связи с массовым применением бэкпропа и под него собственно и делалось

С учетом того, что в 1997 году бэкпроп, конечно, был хорошо известен, но особой популярностью не пользовался. А статьи, упоминающие переобучение, легко находятся и за 1980 год.
Откуда у Вас вообще такая ненависть к этому методу?

(Оффтоп)

tac в сообщении #1708244 писал(а):

когда статистисты влезли не в свою область

Подобные реплики в сочетании с

tac в сообщении #1708228 писал(а):

мне такой формальный язык противоестественен

выглядят не очень хорошо. Вы хотите показать, что какой-то метод хороший - это понятное желание. А вот ругань в адрес умных людей, результаты которых Вы не знаете и не понимаете - хотя и то же понятна, но неприятна.

tac в сообщении #1708244 писал(а):

И только когда, вы признаете феномен

Я не могу признать (или не признать) неизвестно что значащее словосочетание.

tac в сообщении #1708244 писал(а):

я согласится готов с тем, что возникает на практике, а не в умозрительных "мысленных экспериментах".

Мне очень интересно, как Вы собираетесь на практике проверять утверждение для всех возможных датасетов.

tac в сообщении #1708244 писал(а):

на тестовой выборке дает ошибку прогнозирования E $\pm$ de, выше, чем avg (En) , где n - итерация на которой было остановлено обучение, а avg (En) средние ошибок, после n, то он переобучен

Кто на ком стоял?
И раз уж Вы умеете ставить доллары и писать $\TeX$ - то оформляйте формулы. Это, кстати, и по правилам форума требуется.
Кстати, давайте какую-нибудь другую букву для количества итераций, $n$ у нас - размер выхода $S$, которая, насколько я понимаю, фиксирована.
Кстати, итерации тут подразумеваются для решения системы, при фиксированном $k$, или $k$ тоже меняется?

(ещё просьба рисовать на графиках долю ошибок, а не абсолютное число, чтобы можно было, например, сравнивать результаты для разного числа обучающих и тестовых примеров)

[tac]

mihaild в сообщении #1708251 писал(а):

С учетом того, что в 1997 году бэкпроп, конечно, был хорошо известен, но особой популярностью не пользовался.

Ну, скажем так, я сам захватил этот период, и к 2000 г. был сам свидетелем, как бэкпроп был основой обучения у нас на курсе, учитывая что мой бывший научн. руководитель там преподавал лет 20 в качестве профессора, то начиная как и все с перцептрона, он конечно же знал о бэкпропе не позже 1992 года, хотя уверен, что скорее с оригинальной статьи Румельхарда, и конечно же он был популярным в соответствующей среде. Поэтому эти разговоры о переобучении, как минимум с 2001 года слышал не однократно сам.

-- Вт ноя 04, 2025 02:19:15 --

mihaild в сообщении #1708251 писал(а):

Откуда у Вас вообще такая ненависть к этому методу?

Это не ненависть - это избыточность. И не естественность. Да, и не метод это вовсе в смысле нейросетей - это старый градиентный спуск.

-- Вт ноя 04, 2025 02:22:41 --

mihaild в сообщении #1708251 писал(а):

Кто на ком стоял?

Этот вопрос я не понял. Там кажется все четко написано.

-- Вт ноя 04, 2025 02:24:50 --

mihaild в сообщении #1708251 писал(а):

ещё просьба рисовать на графиках долю ошибок, а не абсолютное число, чтобы можно было, например, сравнивать результаты для разного числа обучающих и тестовых примеров)

Это не информативно, а конкретно на этом графике нет результатов для обучающей, только для тестовой.

-- Вт ноя 04, 2025 02:27:17 --

mihaild в сообщении #1708251 писал(а):

Кстати, давайте какую-нибудь другую букву для количества итераций, $n$ у нас - размер выхода $S$, которая, насколько я понимаю, фиксирована.

Ок, итерации, тогда обозначим $t$

-- Вт ноя 04, 2025 02:27:53 --

mihaild в сообщении #1708251 писал(а):

при фиксированном $k$, или $k$ тоже меняется?

Да, фиксированное.

-- Вт ноя 04, 2025 02:32:32 --

1. Полностью обученным перцептроном назовем такой перцептрон, который на обучающей выборке дает количество ошибок $E_{end}$ = 0
2. Если полностью обученный перцептрон на тестовой выборке дает ошибку прогнозирования $E$ $\pm$ $de$, выше, чем AVG ($E_t$) , где $t$ - итерация на которой было остановлено обучение, а AVG ($E_t$) средние ошибок, после $t$ (на отрезке [$t$, $end$]), то он переобучен.
3. Что либо сказать, о неполностью обученном перцептроне нельзя, вследствие не прогнозируемости его поведения.

-- Вт ноя 04, 2025 02:41:27 --

(Оффтоп)

mihaild в сообщении #1708251 писал(а):

А вот ругань в адрес умных людей

это не ругань, это не согласие с их подходом в данной области

-- Вт ноя 04, 2025 03:15:03 --

mihaild в сообщении #1708251 писал(а):

Возьмите любое $n > 100$, сгенерируйте $W_{sa}$ Вашим методом, сгенерируйте $\vec x_i$ бинарные, с $n$ координатами, каждая равна $1$ с вероятностью 90% и $0$ с вероятностью 10%, и возьмите тождественную функцию в качестве $S$. С гигантской вероятностью все $\vec x_i$ получатся разными, а все элементы $\vec x \cdot W_{sa}$ - неположительными.

Это совершенно не так. Возьмем n = 128, а k = 1000. И сгенерируем давайте для начала 10 примеров. Ниже для каждого примера я посчитаю, сколько единиц активируется.

1 - 466
2 - 435
3 - 421
4 - 472
5 - 445
6 - 491
7 - 475
8 - 435
9 - 436
10 - 447

поделим на 2 класса, обучается за 3 итерации.

(Оффтоп)

считайте, где то у вас ошибка

[tac]

Чтобы найти где у нас не сходится, я могу уменьшить k до = 10 (с большой вероятностью этого хватит на этом примере), и показать все примеры и веса. Будете смотреть, или не интересно, где вы ошибаетесь? Можем конечно искать еще более мелкий пример, вырождая его до безобразия, пока он не схлопнится.

Вот 1 входной вектор:

11111110111110111111011111111111110111111011111111111111010111111111011111101101111111111111111111111111111111111101011101111111

-- Вт ноя 04, 2025 03:35:48 --

упс, произошла ошибка у меня ... у меня стоял по умолчанию другой алгоритм генерации весов

[mihaild]

tac в сообщении #1708254 писал(а):

1. Полностью обученным перцептроном назовем такой перцептрон, который на обучающей выборке дает количество ошибок $E_{end}$ = 0
2. Если полностью обученный перцептрон на тестовой выборке дает ошибку прогнозирования $E$ $\pm$ $de$, выше, чем AVG ($E_t$) , где $t$ - итерация на которой было остановлено обучение, а AVG ($E_t$) средние ошибок, после $t$ (на отрезке [$t$, $end$]), то он переобучен.

Непонятно. Если остановили обучение на итерации $t$, то откуда берётся $\text{end} > t$?
(не бойтесь писать формулы целиком, а не заворачивать в доллары каждый символ по отдельности: $E \pm de$, $[t, \text{end}]$ и т.д.)

tac в сообщении #1708254 писал(а):

сколько единиц активируется

Что значит "единица активируется", какая единица?

mihaild в сообщении #1707901 писал(а):

$y = \Theta(\theta(S(\vec x) \cdot W_{sa}) \cdot W_{ar})$

Считаем $S$ тождественной, рассматриваем внутреннюю часть $\theta(\vec x \cdot W_{sa})$.
Размерность $\vec x$ - 128, примерно 115 координат единичные, остальные нулевые. $W_{sa}$ - матрица $128 \times 1000$, сгенерированная алгоритмом выше (каждый столбец содержит примерно 80 минус единиц и примерно 30 единиц). Соответственно при перемножении $\vec x$ на столбец, у нас сумма примерно 72 минус единиц и 27 единиц, т.е. результат перемножения - примерно $-45$. Что после функции Хевисайда превращается в $0$.

tac в сообщении #1708258 писал(а):

я могу уменьшить k до = 10 (с большой вероятностью этого хватит на этом примере), и показать все примеры и веса

Я сам могу. $k = n = 10$

$$A = \begin{pmatrix}-1 & -1 & 1 & -1 & -1 & -1 & 1 & 1 & -1 & -1\\ -1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 & -1 & -1\\ 0 & -1 & -1 & -1 & -1 & -1 & 0 & -1 & -1 & 1\\ -1 & 1 & 0 & -1 & 1 & -1 & 0 & -1 & -1 & 0\\ -1 & -1 & -1 & 0 & 1 & 1 & -1 & -1 & 1 & -1\\ 0 & 1 & 1 & -1 & 1 & -1 & -1 & 0 & -1 & 1\\ -1 & -1 & -1 & 1 & 0 & -1 & 0 & -1 & 1 & -1\\ 0 & -1 & -1 & -1 & 0 & 0 & -1 & 1 & -1 & -1\\ -1 & -1 & -1 & -1 & 0 & 0 & -1 & -1 & -1 & -1\\ 1 & -1 & 0 & -1 & -1 & 1 & -1 & -1 & 0 & -1 \end{pmatrix}$$

$$X = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 \end{pmatrix} $$

(тут взял не случайные, а конкретные с 90% единиц - на размерности 10 дисперсия слишком большая)

$$ X \cdot A = \begin{pmatrix} -4 & -3 & -3 & -6 & 0 & -3 & -6 & -6 & -4 & -4\\ -4 & -5 & -3 & -6 & 0 & -3 & -4 & -4 & -4 & -4\\ -5 & -3 & -1 & -6 & 0 & -3 & -5 & -4 & -4 & -6\\ -4 & -5 & -2 & -6 & -2 & -3 & -5 & -4 & -4 & -5\\ -4 & -3 & -1 & -7 & -2 & -5 & -4 & -4 & -6 & -4\\ -5 & -5 & -3 & -6 & -2 & -3 & -4 & -5 & -4 & -6\\ -4 & -3 & -1 & -8 & -1 & -3 & -5 & -4 & -6 & -4\\ -5 & -3 & -1 & -6 & -1 & -4 & -4 & -6 & -4 & -4\\ -4 & -3 & -1 & -6 & -1 & -4 & -4 & -4 & -4 & -4\\ -6 & -3 & -2 & -6 & 0 & -5 & -4 & -4 & -5 & -4 \end{pmatrix} $$

Все выходы на всех примерах отрицательные.

tac в сообщении #1708258 писал(а):

Будете смотреть, или не интересно, где вы ошибаетесь?

Умерьте апломб.

[tac]

Так тогда чтобы не запутаться еще больше, приведу в одном месте все три

Алгоритм 1: Двухфазная инициализация связей
Вход: SCount = n
Выход: Матрица весов WeightSA
для каждого А-элемента a:
    для j = 1 до 2n:
        сенсор s ← случайный(1, n)
        если j ≤ n:
            вес ← 1  // возбуждающая фаза
        иначе:
            вес ← -1 // тормозящая фаза
        WeightSA[s][a] ← вес

Алгоритм 2: Случайно-чередуемая инициализация связей  
Вход: SCount = n
Выход: Матрица весов WeightSA
для каждого А-элемента a:
    для j = 1 до 2n:
        сенсор ← случайный(1, n)
        тип ← случайный({-1, 1})  // равновероятный выбор
        WeightSA[сенсор][a] ← тип

Алгоритм 3: Двухфазная инициализация связей с накоплением
Вход: SCount = n
Выход: Матрица весов WeightSA
для каждого А-элемента a:
    для j = 1 до 2n:
        сенсор s ← случайный(1, n)
        если j ≤ n:
            вес += 1  // возбуждающая фаза
        иначе:
            вес += -1 // тормозящая фаза
        WeightSA[s][a] ← вес

Алгоритм 4: Ограниченные по диаметру 
Вход: SCount = n
Выход: Матрица весов WeightSA
для каждого А-элемента a:
    для j = 1 до x:
        сенсор ← случайный(1, n)
        WeightSA[сенсор][a] ← +1
    для j = 1 до y:
        сенсор ← случайный(1, n)
        WeightSA[сенсор][a] ← -1

Алгоритм 2 - классический, 1-й - часто работает хорошо, но действительно ваш тест его завалил, алгоритм 3 - это тот с которым я выше спутал

Но кроме классического 2, есть т.н. алгоритмы ограниченные по диаметру (это тоже классика) см. алгоритм 4, которые не решают скажем задачу четности, но легко проходят ваш тест, если принять x=y=32

-- Вт ноя 04, 2025 03:53:36 --

mihaild в сообщении #1708259 писал(а):

тут взял не случайные

и как это понимать :) впрочем не важно, понятно, что вы любите формировать искусственные примеры, которые далеки о практических примеров ...

дополнительные пояснения я дал выше, на большем числе вероятность больше, но действительно этот алгоритм становится не эффективным в этом случае, благо есть из чего выбирать.

[mihaild]

tac в сообщении #1708260 писал(а):

вес += 1 // возбуждающая фаза

А, т.е. в $W_{sa}$ всё же могут быть числа, по модулю большие $1$?
Ладно, у нас есть какая-то случайная матрица $W_{sa}$. Я не думаю, что её точное распределение будет важно, просто меня смутила очевидная асимметрия положительных и отрицательных весов, с учетом того что дальше пороговая функция.

Теперь у нас есть какой-то итеративный алгоритм генерации $W_{ar}$. Мы на каждом шаге $t$ считаем получающуюся ошибку $E_t$ на обучающей выборке. Я пока готов поверить, что для некоторого $T$ будет $E_T = 0$. И мы смотрим на ошибку на каком-то, я не понял каком, шаге на тестовой выборке, и сравниваем её со средней ошибкой на обучающей на каких-то шагах, я опять не понял, на каких.

-- 04.11.2025, 02:00 --

tac в сообщении #1708260 писал(а):

и как это понимать :) впрочем не важно, понятно, что вы любите формировать искусственные примеры

Ну так Вы же говорите, что у Вас замечательный алгоритм, работающий на всех датасетах. А я говорю, что как он работает - это в лучшем случае свойство конкретного рассматриваемого датасета. И как раз предъявление датасета, на котором алгоритм работает плохо, это подтверждает.

[tac]

(Оффтоп)

mihaild в сообщении #1708259 писал(а):

Умерьте апломб.

у вас явно проблемка с пониманием эмоций, было сказано дружественно, с желанием разобраться что произошло, хорошо, что нашел еще до вас. Естественно, когда у меня работает я не предполагаю, что проблема у меня.

-- Вт ноя 04, 2025 04:01:49 --

mihaild в сообщении #1708261 писал(а):

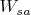
А, т.е. в $W_{sa}$ всё же могут быть числа, по модулю большие $1$?

в классике нет, это моя супер пупер модификация. Кстати, она дает замечательные результаты.

-- Вт ноя 04, 2025 04:10:28 --

mihaild в сообщении #1708261 писал(а):

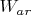
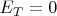
Теперь у нас есть какой-то итеративный алгоритм генерации $W_{ar}$. Мы на каждом шаге $t$ считаем получающуюся ошибку $E_t$ на обучающей выборке. Я пока готов поверить, что для некоторого $T$ будет $E_T = 0$. И мы смотрим на ошибку на каком-то, я не понял каком, шаге на тестовой выборке, и сравниваем её со средней ошибкой на обучающей на каких-то шагах, я опять не понял, на каких.

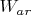
Стоп, стоп ... тут похоже спутались люди и кони ... Вы хотите узнать, как формируются веса $W_{ar}$ ? Потому что дальше, это не связанное с этим, и видимо про мое определение переобучения, что тоже искажено. Но вначале мы хотим разобраться с чем?

-- Вт ноя 04, 2025 04:18:35 --

(Оффтоп)

mihaild в сообщении #1708261 писал(а):

Ну так Вы же говорите, что у Вас замечательный алгоритм, работающий на всех датасетах. А я говорю, что как он работает - это в лучшем случае свойство конкретного рассматриваемого датасета. И как раз предъявление датасета, на котором алгоритм работает плохо, это подтверждает.

Я конечно, рад нашему такому диалогу. Но это пока больше похоже "на формальные придирки" Минского к Розенблатту, только с тем преимуществом что я могу вам ответить. Просто, да у меня есть ... и пока я старался держаться и показывать исключительно классический алгоритм Розенблатта. Я могу бы вам скинуть несколько страниц про то где Розенблатт анализирует как генерировать веса, с тестами и математическими выкладками. А могу показать на скорую руку, как и делаю. А еще вариант, начать показывать не классику, а улучшения такие как алгоритм 3.

Поэтому не спешите и со "своим апломбом"

-- Вт ноя 04, 2025 04:33:55 --

mihaild в сообщении #1708261 писал(а):

И мы смотрим на ошибку на каком-то, я не понял каком, шаге на тестовой выборке

тут все просто, на том же, каждом шаге $t$.

-- Вт ноя 04, 2025 04:37:05 --

mihaild в сообщении #1708261 писал(а):

сравниваем её со средней ошибкой на обучающей на каких-то шагах, я опять не понял, на каких

Потому что мы это не делаем. Вначале мы обучаем до нуля, собирая статистику на тестовой выборке, и только потом мы можем начать анализировать в обратном направлении.

-- Вт ноя 04, 2025 04:47:24 --

tac в сообщении #1708254 писал(а):

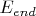
1. Полностью обученным перцептроном назовем такой перцептрон, который на обучающей выборке дает количество ошибок $E_{end}$ = 0
2. Если полностью обученный перцептрон на тестовой выборке дает ошибку прогнозирования $E$ $\pm$ $de$, выше, чем AVG ($E_t$) , где $t$ - итерация на которой было остановлено обучение, а AVG ($E_t$) средние ошибок, после $t$ (на отрезке [$t$, $end$]), то он переобучен.
3. Что либо сказать, о неполностью обученном перцептроне нельзя, вследствие не прогнозируемости его поведения.

Уверен Вы не внимательно прочитали. Кажется, лучше начать заново.

mihaild в сообщении #1708261 писал(а):

Теперь у нас есть какой-то итеративный алгоритм генерации $W_{ar}$.

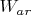
Есть, и пока не важно какой он.

mihaild в сообщении #1708261 писал(а):

Мы на каждом шаге $t$ считаем получающуюся ошибку $E_t$ на обучающей выборке. Я пока готов поверить, что для некоторого $T$ будет $E_T = 0$.

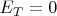
Отлично, тут еще все хорошо.

mihaild в сообщении #1708261 писал(а):

И мы смотрим на ошибку на каком-то, я не понял каком, шаге на тестовой выборке

на том же шаге $t$, но смотрим в смысле собираем историю за каждую итерацию.

mihaild в сообщении #1708261 писал(а):

и сравниваем её со средней ошибкой на обучающей на каких-то шагах

все, абсолютно не так. Вначале мы заканчиваем обучение.

И только потом, мы можем посчитать среднею ошибку (ПРИЧЕМ не обучающей, а тестовой) как сказано на отрезке [$t$, $end$], и построить график - рыжая линия на графике. Среднею ошибку нужно считать $T$ (в моих обозначениях end) раз.

[mihaild]

tac в сообщении #1708262 писал(а):

Вы хотите узнать, как формируются веса $W_{ar}$ ?

Я думал, что в разговоре про шаги Вы как раз говорите о шагах формирования этих весов. Тогда можно пока что не говорить о том, чему они равны в точности, но какие-то их свойства нужны. Или же "шаги обучения" это что-то другое?

tac в сообщении #1708262 писал(а):

на том же шаге $t$

На каком "том же"? $t$ у нас было свободной переменной.
Предлагаю такие обозначения (вроде бы совпадающие с Вашими там, где Вы как-то обозначили):
$t$ - индекс, обозначает шаг
$W_{ar}^t$ - матрица на шаге $t$
$E_t$ - ошибка на обучающей выборке на шаге $t$
$end$ - минимальное число, при котором $E_{end} = 0$; так же известно как "число шагов, на котором заканчиваем обучение"
$E'_t$ - ошибка на тестовой выборке на шаге $t$

tac в сообщении #1708262 писал(а):

Если полностью обученный перцептрон на тестовой выборке дает ошибку прогнозирования $E$ $\pm$ $de$, выше, чем AVG ($E_t$) , где $t$ - итерация на которой было остановлено обучение

Вот тут непонятно. У нас отдельно $end$ - это номер итерации, на которой $E_{end} = 0$. И говорится о "полностью обученном перцептроне", т.е. как раз дающем нулевую ошибку на обучающей выборке. А что тогда такое "итерация, на которой остановлено обучение", и чем она отличается от $end$?