Здравствуйте, уважаемые форумчане!Будьте добры, подскажите, пожалуйста.
В задаче просят найти все

и

, при которых система имеет
не менее 5 решений.
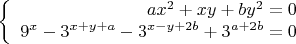
Может быть, я чего-то не вижу, но красивого решения как будто нет, надо "в лоб".
Первое уравнение заменой
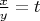
сводится к квадратному
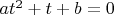
, откуда получается, что дискриминант
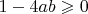
и один или два корня. Отдельно, наверно, надо подумать про случаи

и

.
А вот что делать со вторым уравнением, я не совсем понимаю. Предположим, что из замены можно выразить

и подставить. Получится
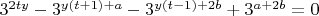
Можно ещё (но нужно ли)
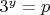
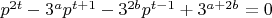
Много букв, что делать непонятно...