Интеграл
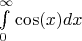
считается расходящимся,
также как и 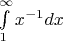
. Сейчас занимаюсь построением кривых в пространстве, там много интегралов от кривизны, кручения и их комбинаций.
Мне было бы важно
разделить эти типы поведения. Лично я бы назвал
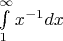
сходящимся к
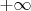
, а скажем
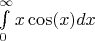
- сходящимся к

по абсолютному значению.
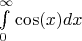
можно назвать как-то по другому: не имеющий предела, неоднозначный и т.д.
Уверен, что можно дать и строгое определение "сходимости к

", типа для любого
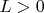
существует
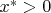
такое, что
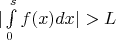
для любого

Есть ли подобные определения в анализе? Как они называются по-английски? (важно для дискуссии на Mathematica SE). Может быть не в строгих курсах, но неужели никто не делал акцент на том, что это совершенно разное поведение?