Уважаемые участники форума! Помогите, пожалуйста, разобраться с доказательством алгебраической леммы из работы
Rantzer. On the Kalman—Yakubovich—Popov lemma. Это, конечно, не учебная задача, но аппарат используется стандартный. Вот формулировка леммы и ее доказательство из статьи.
Lemma 3. Let

and

be complex matrices of the same size. Then
(i)
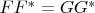
if and only if there exists a matrix

such that

and
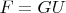
.
(ii)
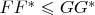
if and only if there exists a matrix

such that

and
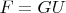
.
(iii)
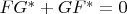
if and only if there exists a matrix

such that

and
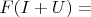
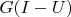
.
(iv)
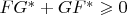
if and only if there exists a matrix

such that

and
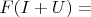
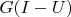
.
Proof of Lemma 3.
(Оффтоп)
The statements (iii) and (iv) follow from (i) and (ii) respectively, by replacement of

and

with

and

.
It remains to prove (i) and (ii). Let the size of

and

be
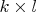
. Consider first (i) for square matrices, i.e. the case

. Assuming that
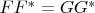
, introduce the polar decompositions\\
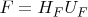
,\\
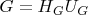
,\\
where
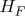
and
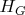
are hermitian and positive semidefinite, while
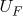
and
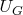
are unitary. Then
![\[
H_{F}=\left(F F^{*}\right)^{1 / 2}=\left(G G^{*}\right)^{1 / 2}=H_{G}
\] \[
H_{F}=\left(F F^{*}\right)^{1 / 2}=\left(G G^{*}\right)^{1 / 2}=H_{G}
\]](https://dxdy-04.korotkov.co.uk/f/3/9/7/397e15a37b61052d714fc09dfdbd4e2b82.png)
so the unitary matrix
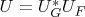
satisfies
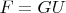
.
The case

follows immediately by extending

and

with zero rows to square matrices.
If

, then let

be a submatrix of

with the same rank, but a minimal number of rows. Let

be defined by the corresponding rows in

. Then
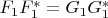
and existence of a unitary matrix

such that
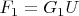
follows as above. In fact, since all rows of

and

are linear combinations of the rows in

and

, the desired equality
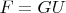
is proved as well.
To prove (ii) from (i), note that
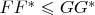
, if and only if there exists an

such that
![$[F H][F H]^{*}=$ $[F H][F H]^{*}=$](https://dxdy-03.korotkov.co.uk/f/e/0/f/e0fbe744f9bdbbd5195f0dff4cbf492382.png)
![$\left[\begin{array}{ll}G & 0\end{array}\right]\left[\begin{array}{ll}G & 0\end{array}\right]^{*}$ $\left[\begin{array}{ll}G & 0\end{array}\right]\left[\begin{array}{ll}G & 0\end{array}\right]^{*}$](https://dxdy-04.korotkov.co.uk/f/f/3/4/f34473c2fee5005e90146758148d25ba82.png)
. By (i), this is equivalent to existence of

and a unitary matrix
![\[
\left[\begin{array}{ll}U & V \\ V^{*} & W\end{array}\right]
\] \[
\left[\begin{array}{ll}U & V \\ V^{*} & W\end{array}\right]
\]](https://dxdy-02.korotkov.co.uk/f/1/7/0/1707b6ad1a5c03e0782cfbac2f3d912182.png)
such that
![\[
\left[\begin{array}{ll}F & H\end{array}\right]=\left[\begin{array}{ll}G & 0\end{array}\right]\left[\begin{array}{ll}U & V \\ V^{*} & W\end{array}\right]
\] \[
\left[\begin{array}{ll}F & H\end{array}\right]=\left[\begin{array}{ll}G & 0\end{array}\right]\left[\begin{array}{ll}U & V \\ V^{*} & W\end{array}\right]
\]](https://dxdy-01.korotkov.co.uk/f/8/d/4/8d46efc84d2daf3340e55d8f4d8b8cdf82.png)
Such matrices exist if and only if
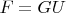
and
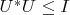
so (ii) is proved.
Вопрос 1. Зачем при доказательстве утверждения (i) отдельно рассматриваются случаи

и

, причем по-разному? Я рассуждаю так. Пусть

. Тогда дополним обе матрицы нулями и получим
![\[
\left[\begin{array}{l}F \\ 0\end{array}\right]\left[\begin{array}{ll}F^* & 0\end{array}\right] =
\left[\begin{array}{l}G \\ 0\end{array}\right]\left[\begin{array}{ll}G^* & 0\end{array}\right],
%[F H][F H]^{*}=\left[\begin{array}{ll}G & 0\end{array}\right]\left[\begin{array}{ll}G & 0\end{array}\right]^{*}
\] \[
\left[\begin{array}{l}F \\ 0\end{array}\right]\left[\begin{array}{ll}F^* & 0\end{array}\right] =
\left[\begin{array}{l}G \\ 0\end{array}\right]\left[\begin{array}{ll}G^* & 0\end{array}\right],
%[F H][F H]^{*}=\left[\begin{array}{ll}G & 0\end{array}\right]\left[\begin{array}{ll}G & 0\end{array}\right]^{*}
\]](https://dxdy-02.korotkov.co.uk/f/d/6/9/d69ce892bbeb70de5cb8d02e6490c31582.png)
так как
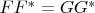
.
Тогда
![\[
\left[\begin{array}{l}F \\ 0\end{array}\right] = H_FU_F, \ \left[\begin{array}{l}G \\ 0\end{array}\right] = H_GU_G
\] \[
\left[\begin{array}{l}F \\ 0\end{array}\right] = H_FU_F, \ \left[\begin{array}{l}G \\ 0\end{array}\right] = H_GU_G
\]](https://dxdy-04.korotkov.co.uk/f/b/4/d/b4dbb1698407f0a1312d53b0d2a9e89382.png)
и
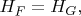
далее аналогично квадратному случаю.
Если

, то
![\[
\left[\begin{array}{ll}F & 0\end{array}\right]\left[\begin{array}{ll}F & 0\end{array}\right]^{*}=FF^*=GG^* = \left[\begin{array}{ll}G & 0\end{array}\right]\left[\begin{array}{ll}G & 0\end{array}\right]^{*}
\] \[
\left[\begin{array}{ll}F & 0\end{array}\right]\left[\begin{array}{ll}F & 0\end{array}\right]^{*}=FF^*=GG^* = \left[\begin{array}{ll}G & 0\end{array}\right]\left[\begin{array}{ll}G & 0\end{array}\right]^{*}
\]](https://dxdy-01.korotkov.co.uk/f/8/b/c/8bca735f5430706e8b1380ede7fb138c82.png)
и снова аналогично. Есть ли здесь ошибка?
Вопрос 2. В последнем переходе "Such matrices exist if and only if
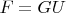
and
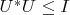
" мне не понятно, как в части "if" получить существование большой унитарной матрицы.
Спасибо!