Бинарная гипотеза Гольбаха.
Гипотеза Гольдбаха (проблема Эйлера, бинарная проблема Гольдбаха) утверждение о том, что любое чётное число, начиная с 4, можно представить в виде суммы двух простых чисел.
В данной работе осуществлен плавный переход, от поиска пар простых чисел, дающих в сумме (N), к поиску пар составных чисел вида 6к-1 или 6к +1, так же дающих в сумме N. И в дальнейшем обратных переход, через формулу связывающие два этих представления.
Поиск минимального количества пар составных чисел, осуществляется путем нахождения количества пар чисел, дающих в сумме (N). в которых одно слагаемое кратно 5 а другое любому простому числу, не превосходящее корня из N , далее все возможные количества, полученные всеми возможными комбинациями , суммируются, а повторы пар исключаются.
Формулы, которые потребуются для доказательства.
N mod 6 = 0
x-количество уникальных пар чисел (вида 6k + 1 или 6k – 1), которых дают в сумме N и состоят из составных чисел
h(N) -сколькими способами можно представить число N в виде суммы двух простых (вида 6k + 1 или 6k – 1).
N- Чётное натуральное число кратное 6.
π(N)-количества простых до N
P – простое число
С – составное число
при N-1=C
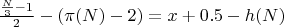
при N-1=P
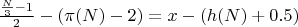
Далее опишу, как эти формулы выводятся. (на примере N-1=P)
Очевидно, что количество простых (больше трех) чисел до N равняется:
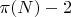
Все эти простые числа распределены между, парами из простых чисел, дающих в сумме (N), и парами где одно число простое, а другое составное.
+1 – простое число которому не досталось пары.
Формула 1.
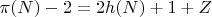
Количество всех представлений из простых и составных.
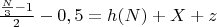
Выразим из первой формулы чему равно Z.
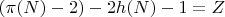
Подставим во второе уравнение.
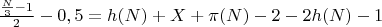
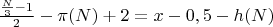
Количество чисел вида 6к-1 и 6к+1 до N.
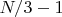
Так, как все числа вида 6к-1 и 6к+1 до N имеют остатки деления на 6 равные 1 и -1, из всех возможных остатков 1 2 3 4 5 0, лишь два из шести нам подходят. (исключение 1, которая так же имеет остаток 1)
Пример использования.
N= 4 124 322
π(N)=291341
X= 424199
h(N)=28151
при 4 124 322-1=P
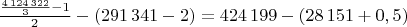
Далее я приведу еще пару формул, после расскажу, как они выводятся.
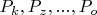
Поиск минимального количества пар составных чисел, осуществляется путем нахождения количества пар чисел, дающих в сумме (N). в которых одно слагаемое кратно 5 а другое любому простому числу, не превосходящее корня из N , далее все возможные количества, полученные всеми возможными комбинациями , суммируются, а повторы пар исключаются.
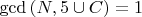
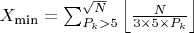
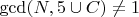
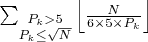
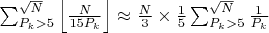
Способ найти количество представлений числа N в виде суммы двух составных чисел, (которые имеют вид 6k-1 или 6k+1) в которых одно из слагаемых делится на P1 а другое на P2.
P1 < P2
Где P1 и P2 простые числа > 3.
Если одно число из пары делится на 5, а другое на 7, тогда следующая такая пара встретиться через 5*7*6, но это пары, в которых первое слагаемое делится на 5, а у нас еще есть пары, в которых первое слагаемое делится на 7.
тогда формула превращается в 5*7*3
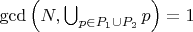
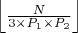
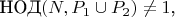
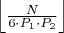
Например:
N = 31416
P_1=17
P_2=101
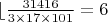
Проверено кодом в питоне.
Исходя из того, что сумма обратных простых бесконечна, при больших значениях N, всегда выполняется неравенство.
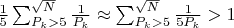
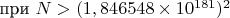
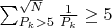
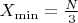
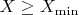
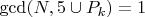
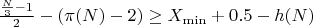
при N-1=C
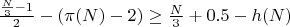
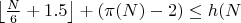
при N-1=P
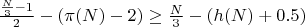
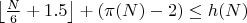
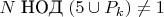
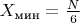
при N-1=C
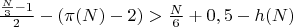
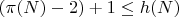
при N-1=P
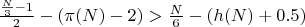
![$\[ (\pi(N) - 2) \leq h(N) \]$ $\[ (\pi(N) - 2) \leq h(N) \]$](https://dxdy-01.korotkov.co.uk/f/0/9/f/09f9fd164d1808494ae84609ae40a8a382.png)
Поскольку количество пар простых чисел, дающих в сумме N, для чисел больше (1,846548×10181) 2
) всегда больше 0, делаем вывод, что гипотеза Гольбаха для чисел кратных 6, верна.
N mod 6 =2 v 4
x-количество пар чисел (вида 6k + 1 или 6k – 1), которых дают в сумме N и состоят из составных чисел
h(N) -сколькими способами можно представить число N в виде суммы двух простых
N- Чётное натуральное число, имеющее остаток от деления на 6 равный либо 2, либо 4.
π(N)-количества простых до N
Tc - Количество составных чисел вида (6к-1 или 6к+1), не участвующих в образовании пар.
Tp - Количество простых чисел вида (6к-1 или 6к+1), не участвующих в образовании пар.
Ac- На сколько количество составных чисел вида (6к+1), превышает количество составных чисел вида (6к-1), на интервале от 1 до N.
Ap- На сколько количество составных чисел вида (6к+1), превышает количество составных чисел вида (6к-1), на интервале от 1 до N.
Упрощённая формула с погрешностью +-3.
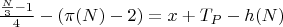
Пример использования.
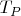
-Примерное количество
N Mod (6) =2
![$\[ T_p = \frac{\pi(N) - 2}{2} - \frac{A_p}{2} \]$ $\[ T_p = \frac{\pi(N) - 2}{2} - \frac{A_p}{2} \]$](https://dxdy-01.korotkov.co.uk/f/8/a/1/8a17d46a41c1cc51a1bb72cc71c5c39a82.png)
N Mod (6) =4
![$\[ T_p = \frac{\pi(N) + 2}{2} + \frac{A_p}{2} \]$ $\[ T_p = \frac{\pi(N) + 2}{2} + \frac{A_p}{2} \]$](https://dxdy-04.korotkov.co.uk/f/f/5/9/f590871cc6b4c5279e6b9ef82945fa3982.png)
N= 315842
π(N)=27261
X= 14310
h(N)=1599
T_c= 38990
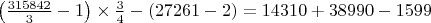
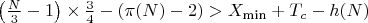
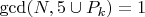
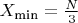
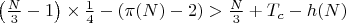
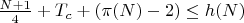
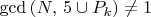
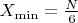
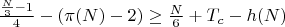
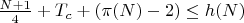
Поскольку минимальное количество пар простых чисел, дающих в сумме N, для чисел больше ((1,846548×10181) 2, всегда больше 0, делаем вывод, что гипотеза Гольбаха верна.
Гипотеза верна для больше (1,846548×10181) ^2