А вот без категорий и функторов. Встретилось это понятие без объяснения в доказательстве нужного мне утверждения. Странно, что в интернете нигде не встречается больше такого термина. Если коротко, выглядит это так: Пусть

- комплексно аналитическое многообразие и
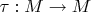
--- вещественная структура на нем (т.е. антиголоморфная инволюция). Пусть

- пучок ростков голоморфных комплекснозначных функций на
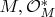
- пучок ростков голоморфных комплекснозначных функций, не обращающихся в нуль. На пучках
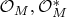
имеется каноническая вещественная структура, которая задается правилом
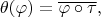
где

- росток функции, а черта означает комплексное сопряжение.
Пусть
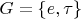
- группа второго порядка. Далее следует описание группы когомологии Галуа-Гротендика
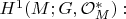
пусть
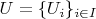
- покрытие многообразия

причем

действует на множество индексов

таким образом, что
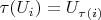
для всякого
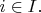
В этом случае покрытие

называется

-покрытием. Оно будет называться покрытием без неподвижных точек, если

действует на

без неподвижных точек.
Пусть

---

-покрытие без неподвижных точек. Тогда рассмотрим комплекс коцепей
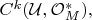
на нем действует инволюция

по правилу: если
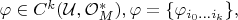
то
![$$[\tau(\varphi)]_{i_0...i_k}=\theta(\varphi_{\tau(i_0)...\tau(i_k)}).$$ $$[\tau(\varphi)]_{i_0...i_k}=\theta(\varphi_{\tau(i_0)...\tau(i_k)}).$$](https://dxdy-01.korotkov.co.uk/f/8/c/2/8c23065b5091203a63b584583b1f96d582.png)
Положим
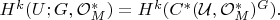
Тогда
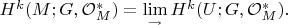
Вот как-то так.