Сейчас это, с одной строны красивое выражение, с другой стороны кажется банальным и очевидным, также как
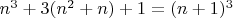
Но для увеличения ребра гиперкуба (размерности

) на

действительно вроде бы получается
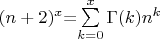
, где

- число граней размерности

.
Для меня выглядит очень даже небанально. Но я всяко не авторитет...