Есть ли свойства у такой матрицы?

[limtv]

Дана некоторая (прям-льная или кв-ая) матрица, для которой сумма элементов каждого столбца и каждой строки равна 0.

Есть ли какие либо специфичечкие свойства у данной матрицы?

Я сам весьма далек от лин. алгебры и не могу провести даже элементарное исследование, но эта задача встала ребром в моей жизни и я очень прошу сообщить любые сведения о данном типе матриц, если в них есть хоть что-нибудь примечательное.

Буду очень благодарен за помощь.

[sydorov]

Как минимум две строки и два столбца являются линейно зависимыми

[lel0lel]

sydorov в сообщении #1704457 писал(а):

Как минимум две строки и два столбца являются линейно зависимыми

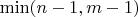
Почему именно две? Просто строки и столбцы матрицы линейно зависимые, ранг не больше $\min(n-1, m-1)$. Размерность линейного подпространства таких матриц равна $(n-1)\times(m-1)$.

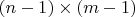
-- Сб окт 04, 2025 20:29:24 --

limtv в сообщении #1704452 писал(а):

Есть ли какие либо специфичечкие свойства у данной матрицы?

Прямо чтобы очень специфических -- нет. Считайте, что произвольная такая матрица это таблица $n\times m$, в которой вы вправе заполнить любыми элементами всё, кроме первой строки и первого столбца. А вот их уже записать, чтобы выполнялись условия. В итоге, вы будете знать, что ядру отображения и транспонированного отображения принадлежат вектора состоящие из единиц длины $m$ и $n$, соответственно.

-- Сб окт 04, 2025 20:45:56 --

Всё-таки примечательное свойство есть) Любой элемент $a_{i,j}$ такой матрицы равен сумме всех элементов в матрице, получающейся из исходной, вычёркиванием $i$-ой строки и $j$-го столбца. Собственно, это также справедливо для любой суммы элементов, она равна сумме элементов матрицы, получающейся вычёркиванием строк и столбцов, с индексами как у элементов в исходной сумме. Доказывается это легко, ведь сумма всех элементов матрицы равна нулю.

[Утундрий]

limtv в сообщении #1704452 писал(а):

прям-льная

limtv в сообщении #1704452 писал(а):

кв-ая

limtv в сообщении #1704452 писал(а):

лин.

Что вы будете дел. со всем этим сэконом. врем. ?