Разложение дроби на простейшие над R

[EminentVictorians]

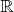
Я хочу доказать теорему, что любую правильную рациональную дробь над $\mathbb R$ можно представить в виде конечной суммы простых дробей. Доказать хочу сам, без учебника. В принципе, я достаточно неплохо продвинулся, остался практически один шаг, но у меня не получается его сделать. Напишу весь ход мысли.

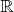
Тот факт, что над $\mathbb R$ неприводимые многочлены сводятся к линейным и квадратичным с отрицательным дискриминантом предполагается известным.

Пункт 0
Для начала я ограничусь дробями, у которых в знаменателе лишь 2 множителя. Есть 3 варианта таких дробей, в зависимости от того, что в знаменателе:

1)Две степени линейных многочленов.
2)Одна степень линейного и одна степень квадратичного (с отрицательным дискриминантом, разумеется)
3)Две степени квадратичных


Пункт 1
Рассмотрим первый вариант: в знаменателе две степени линейных многочленов. Без ограничения общности, числитель можно считать единицей. Короче говоря, надо преобразовать такую дробь:

$$\frac{1}{(x+a)^m(x+b)^n}$$

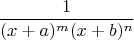
Я заметил, что её получается разложить в 2 дроби такие, что в первой - первая степень на единицу меньше, а во второй - вторая. Лучше написать формулой:

$$\frac{1}{(x+a)^m(x+b)^n} = \frac{A}{(x+a)^{m-1}(x+b)^n} + \frac{B}{(x+a)^m(x+b)^{n-1}}$$

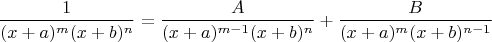
где $A$ и $B$ - просто какие-то числа.
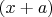
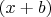
У первой дроби дополнительный множитель $(x + a)$, у второй $(x+b)$. То есть, чтобы определить $A$ и $B$, надо решить такое уравнение:

$$A(x+a) + B(x+b) = 1$$

$$Ax+aA + Bx+bB = 1$$

$$(A+B)x + (aA + bB) = 1$$

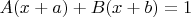
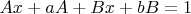
Учитывая, что в правой части у нас многочлен нулевой степени, получаем следующую систему:

$$\left\{ \begin{array}{rcl} A + B &=& 0 \\ aA + bB &=& 1\\ \end{array} \right.$$

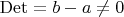
Дальше можно решать её в лоб, выражая одну переменную через другую, но проще найти определитель матрицы коэффициентов: $\operatorname{Det} = b - a \ne 0$ (разумеется $a$ и $b$ считаются различными, иначе первоначальная дробь уже была бы простейшей). Определитель не ноль $\Rightarrow$ СЛАУ имеет решение (по теореме Кронекера-Капелли). Все, мы смогли разложить дробь первого типа в сумму двух таких же, но со степенями меньше. Дальше по индукции можно и каждую из полученных точно так же раскладывать, вплоть до простейших. Здесь существенно, что в числителях при разложении получились именно числа, а не какие-то более крупные многочлены.


Шаг 2
Пусть теперь раскладываемая дробь имеет в знаменателе одну степень линейного и одну степень квадратичного многочленов. Опять без уменьшения общности можно считать, что в числителе стоит единица.
Докажем, что её можно разложить вот так:

$$\frac{1}{(x+a)^m(x^2 + px + q)^n} = \frac{Ax + B}{(x+a)^{m-1}(x^2 + px + q)^n} + \frac{C}{(x+a)^m(x^2 + px + q)^{n-1}}$$

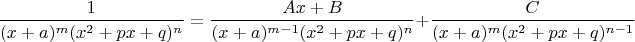
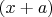
У первой дроби дополнительный множитель $(x + a)$, у второй $(x^2 + px + q)$.
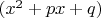
Получаем следующее уравнение:

$$(Ax + B)(x+a) + C(x^2 + px + q) = 1$$

$$Ax^2 + aAx + Bx + aB + Cx^2 + pCx + qC = 1$$

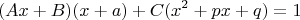
Опять в правой части многочлен нулевой степени, значит имеем такую систему:

$$\left\{ \begin{array}{rcl} A + C &=& 0 \\ aA + B + pC &=& 0\\ aB + qC &=& 1\\ \end{array} \right.$$

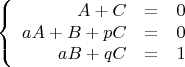
Выразим $C$ через $A$ из первого уравнения: $C = -A$.
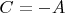
Тогда:

$$\left\{ \begin{array}{rcl} -aC + B + pC &=& 0\\ aB + qC &=& 1\\ \end{array} \right.$$

$$\left\{ \begin{array}{rcl} B + (p-a)C &=& 0\\ aB + qC &=& 1\\ \end{array} \right.$$

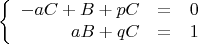
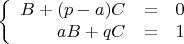
Опять найдем определитель:

$$\operatorname{Det} = q - a(p-a) = q + a(a-p) = q + a^2 - ap = a^2 -ap + q$$

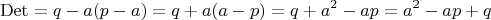
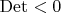
Если посмотреть на получившуюся штуку как на многочлен от одной переменной $a$, то замечаем, что его дискриминант равен $p^2 - 4q$, а это в точности дискриминант квадратичного многочлена из знаменателя раскладываемой дроби, а он по условию отрицательный. Это значит, что при любом $a$ наш $\operatorname{Det} < 0$, но главное, что он не ноль, а значит опять по теореме Кронекера-Капелли существует решение нашей СЛАУ и мы смогли разложить ту дробь, которую хотели в этом пункте. Кстати, числители в этом разложении тоже получились "небольшие": один линейный, другой - просто число. Это тоже существенно.

Шаг 3
Осталось доказать, что можно разложить дробь вот такого типа:

$$\frac{ax + b}{(x^2 + qx + p)^m(x^2 + sx + w)^n}$$

По аналогии с первыми двумя пунктами, я попытаюсь разложить её на две вот такие дроби (тоже с "небольшими" числителями):

$$\frac{ax + b}{(x^2 + qx + p)^m(x^2 + sx + w)^n} = \frac{Ax + B}{(x^2 + qx + p)^{m-1}(x^2 + sx + w)^n} + \frac{Cx + D}{(x^2 + qx + p)^m(x^2 + sx + w)^{n-1}}$$

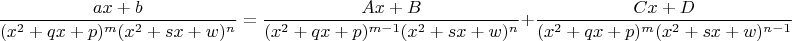
И здесь у меня возникает проблема, не получается это сделать. Напишу, как я делал.

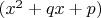
У первой дроби дополнительный множитель $(x^2 + qx + p)$, у второй $(x^2 + sx + w)$.
Составим уравнение:

$$(Ax + B)(x^2 + qx + p) + (Cx + D)(x^2 + sx + w) = ax + b$$

$$Ax^3 + qAx^2 + pAx + Bx^2 + qBx + pB + Cx^3 + sCx^2 + wCx + Dx^2 + sDx + wD = ax + b$$

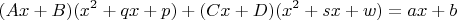
Опять составим СЛАУ:

$$\left\{ \begin{array}{rcl} A + C &=& 0\\ qA + B + sC + D &=& 0 \\ pA + qB + wC + sD &=& a \\ pB + wD &=& b \\ \end{array} \right.$$

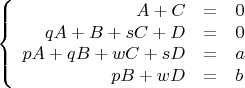
Опять выразим $A$ через $C$: $A = -C$.

$$\left\{ \begin{array}{rcl} -qC + B + sC + D &=& 0 \\ -pC + qB + wC + sD &=& a \\ pB + wD &=& b \\ \end{array} \right.$$

$$\left\{ \begin{array}{rcl} B + (s-q)C + D &=& 0 \\ qB + (w-p)C + sD &=& a \\ pB + wD &=& b \\ \end{array} \right.$$

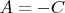
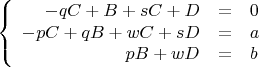
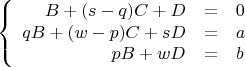
Чтобы вычислить определитель этой матрицы коэффициентов (которая 3 на 3), я решил разложить его по последней строке:

$$\operatorname{Det} = p((s-q)s - (w-p)) + w((w-p) - q(s-q)) = p(s^2 - qs - w + p) + w(w - p - qs + q^2) = $$

$$ = ps^2 - qps - wp + p^2 + w^2 - pw - qws + wq^2 = $$

$$ = p^2 - pw - wp + w^2 + ps^2 - qps - qws + wq^2 = (p-w)^2 + ps(s - q) - qw(s - q) =$$

$$ = (p-w)^2 + (ps - qw)(s-q)$$

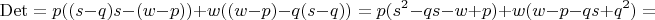
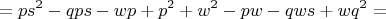
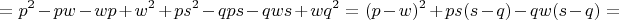
И что делать дальше? Как доказать, что эта штука - не ноль?
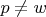
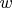
Понятно, что если $s = q$, то $p \ne w$, значит первое слагаемое будет строго положительным, а второе нулем, значит вся сумма не ноль. Так же понятно, что каждый $p$ и $w$ не нули. Но этого мало, чтобы доказать ненулевость получившегося определителя.
В учебник смотреть не хочу, у меня азарт довести это доказательство до ума.
Что дальше делать?

[dgwuqtj]

У вас на переменные есть только ограничения $q^2 < 4 p$, $s^2 < 4 w$ и $(q, p) \neq (s, w)$, так что как-то из них должно выводиться. Но тут можно просто считать (сделав линейную замену), что $q = 0$, тогда всё очевидно.

[Rak so dna]

EminentVictorians в сообщении #1703093 писал(а):

$$ = (p-w)^2 + (ps - qw)(s-q)$$

И что делать дальше? Как доказать, что эта штука - не ноль?

$$(p-w)^2 + (ps-qw)(s-q)=\frac{1}{16}(s-q)^4 + \frac{1}{8}\left((4p-q^2)+(4w-s^2)\right)(s-q)^2+\frac{1}{16}\left((4p-q^2)-(4w-s^2)\right)^2$$

[EminentVictorians]

Rak so dna в сообщении #1703103 писал(а):

$$(p-w)^2 + (ps-qw)(s-q)=\frac{1}{16}(s-q)^4 + \frac{1}{8}\left((4p-q^2)+(4w-s^2)\right)(s-q)^2+\frac{1}{16}\left((4p-q^2)-(4w-s^2)\right)^2$$

Обалдеть... Никогда бы не смог до такого додуматься. Как вы это равенство получили? Руками или какая-то система компьютерной алгебры?

[Rak so dna]

Пусть $f(p,w) = (p-w)^2+(ps-qw)(s-q)$, тогда:

$f\left(\dfrac{q^2}{4},\dfrac{s^2}{4}\right)=\dfrac{1}{16}(s-q)^4$

и

$f\left(x+\dfrac{q^2}{4},y+\dfrac{s^2}{4}\right) - f\left(\dfrac{q^2}{4},\dfrac{s^2}{4}\right)=(x-y)^2+\dfrac12(s-q)^2(y+x)$

осталось только заменить $x\rightarrow p-\dfrac{q^2}{4},~y\rightarrow w-\dfrac{s^2}{4}$

[Padawan]

EminentVictorians
Пусть $\frac{h}{fg}$ -- правильная рациональная дробь, у которой $(f,g)=1$. Тогда существуют многочлены $u,v$ такие, что $uf+vg=1$. Тогда

$$ \frac{h}{fg}=\frac{hv}{f}+\frac{hu}{g}. $$

Поступая так, мы разложим исходную дробь на сумму дробей вида $\dfrac{p}{f^n}$, где $f$ -- неразложимый многочлен ($f(x)=x+a$ или $f(x)=x^2+ax+b$ в случае многочленов над полем $\mathbb R$). Выделив целую часть в каждой такой дроби, можно считать, что $\deg p<\deg f^n$ (и все целые части взаимно уничтожатся, так как исходная дробь правильная). Далее делим с остатком $p$ на $f$: $p=fq+r$, $\deg r<\deg f$. Получим

$$ \frac p{f^n}=\frac q{f^{n-1}}+\frac r{f^n}, $$

где дробь $\dfrac q{f^{n-1}}$ тоже правильная
Таким образом, каждую дробь $\dfrac{p}{f^n}$ мы сможем представить в виде суммы дробей $$\frac{r_1}{f}+\frac{r_2}{f^2}+\ldots+\frac{r_n}{f^n},$ где $\deg r_i<\deg f$ для всех $i=1,\ldots, n$.