Условные вероятности и "условные события"

[Anton_Peplov]

Вопрос навеян темой «Неравенство Белла», но я полностью сформулирую задачу здесь в стартовом посте. В конце концов, она мне интересна и сама по себе.

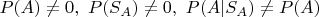
Алиса решает, провести ли ей отпуск на курорте (событие $A$) или дома. На ее решение может повлиять тот факт, дадут ли ей премию (событие $S_A$). По условию $P(A) \ne 0, \ P(S_A) \ne 0, \ P(A| S_A) \ne P(A)$. Все вышесказанное верно и для Боба. Его отдых на курорте - событие $B$, его премия - событие $S_B$.

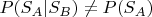
Алиса и Боб работают в одной фирме, так что события $S_A$ и $S_B$ (получение премий) зависят друг от друга: $ P(S_A| S_B) \ne P(S_A)$. Поэтому события $A$ и $B$ (отдых на курорте) тоже зависят друг от друга: $P(A|B) \ne P(A)$.

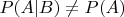
Условие единственности связи: Алиса и Боб не знакомы друг с другом, не имеют общих знакомых, живут в разных городах и т.д. Единственная связь между их решениями поехать на курорт или остаться дома – через связь между возможной выплатой им премий.

Вопрос: требуется математически формализовать условие единственности связи на языке теории вероятностей.

Интуиция подсказывает, что это условие формализуется в виде

$$ P[(A, B)|(S_A, S_B)] = P(A|S_A) P(B|S_B) \eqno{(1)} $$

Но я не могу обосновать эту формализацию.

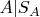
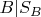
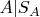
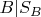
Уважаемый lel0lel подсказывает: нужно, чтобы события $A|S_A$ и $B|S_B$ были независимыми. Но можно ли вообще говорить о событиях $A|S_A$ и $B|S_B$? Что такое условная вероятность – это я понимаю, а вот как насчет условных событий?

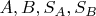
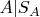
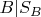
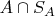
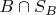
Если спускаться до оснований, то мы взяли множество элементарных исходов $\Omega$ и определили сигма-алгебру $\Gamma$ его подмножеств, среди которых события $A, B, S_A, S_B$. Но в ней нет событий $A|S_A$ и $B|S_B$. События $A \cap S_A$ и $B \cap S_B$ - это не то же самое, т.к., вообще говоря, $P(A S_A) \ne P(A|S_A)$.

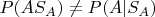
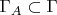
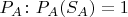
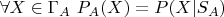
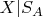
Можно взять событие $S_A$ в качестве нового множества элементарных исходов, взять некоторую сигма-алгебру $\Gamma_A \subset \Gamma$ его подмножеств и ввести на ней вероятность $P_A \colon P_A(S_A)=1$. Вроде бы тогда получается $\forall X \in \Gamma_A \ P_A(X) = P(X|S_A)$ и в этом смысле можно говорить, что мы определили сигма-алгебру, элементами которой являются условные события $ X|S_A$. Но элементами этой сигма-алгебры не будут ни $A$, ни $B$, ни уж тем более $B|S_B$.

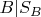
У меня ощущение, что я упускаю что-то очевидное. Может быть, можно как-то иначе обосновать переход от условия единственности связи к уравнению (1)?

Я хочу, чтобы все было понятно на уровне сигма-алгебр, чтобы убедиться, что нигде нет логической ошибки.

[dsge]

Anton_Peplov в сообщении #1702486 писал(а):

Что такое условная вероятность – это я понимаю, а вот как насчет условных событий?

Anton_Peplov в сообщении #1702486 писал(а):

Я хочу, чтобы все было понятно на уровне сигма-алгебр, чтобы убедиться, что нигде нет логической ошибки.

Первичным понятием является условное матожидание, которое есть случайная величина, определенная на подсигма-алгебре, которая идет после вертикальной черточки. Условная вероятность получается как условное матожидание от индикаторной функции. Подсигма-алгебра также определяется, как порожденная другой случайной величиной. В вашем примере можно определить все случайные величины (А, В), принимающие значения ${0, 1}$.
В учебнике Ширяева дано хорошее изложение этого материала.

[mihaild]

Довести до сигма-алгебр это, конечно, можно, но ИМХО занятие по полезности сравнимое с доведением определения интеграла до кодирования вещественных чисел множествами.

Anton_Peplov в сообщении #1702486 писал(а):

$P[(A, B)|(S_A, S_B)] = P(A|S_A) P(B|S_B) \eqno{(1)}$

Когда мы рассуждаем о независимости нескольких событий, одного равенства уже недостаточно. Из $P(A | B) = P(A)$ следуют все оставшиеся комбинации, например $P(\neg B | A) = P(\neg B)$. А вот из Вашего равенства уже не следует, например, $P((A, B) | (S_A, \neg S_B)) = P(A | S_A) P(B | \neg S_B)$ - а, наверное, хотелось бы.
Введём обозначение: $A \perp\!\!\!\perp B | C$ - "$A$ не зависит от $B$ при условии $C$" - означающий $P(A|BC) = P(A|C)$.
Выполнены очевидные свойства: $A \perp\!\!\!\perp B | C \leftrightarrow B \perp\!\!\!\perp A | C \leftrightarrow \neg A \perp\!\!\!\perp B | C$.
Вам нужно, видимо, что-то вроде $A \perp\!\!\!\perp B | S_A^\alpha S_B^\beta$ для $\alpha, \beta \in \{0, 1\}$.

Кстати в причинных диаграммах эта ситуация сообщается очень просто :)
$\begin{tikzpicture} % Define common styles for nodes and arrows \tikzstyle{mynode} = [draw, rectangle, minimum size=1cm, text width=2.5cm, text centered] \tikzstyle{arrow} = [->, >=stealth] % Top row nodes (y=4) \node[mynode] (alice_mood) at (-4, 4) {Alice's mood}; \node[mynode] (econ) at ( 0, 4) {economy situation}; \node[mynode] (bob_mood) at ( 4, 4) {Bob's mood}; % Middle row nodes (y=2) \node[mynode] (SA) at (-2, 2) {$S_A$}; \node[mynode] (SB) at ( 2, 2) {$S_B$}; % Bottom row nodes (y=0) \node[mynode] (A) at (-2, 0) {A}; \node[mynode] (B) at ( 2, 0) {B}; % Draw the arrows \draw[arrow] (alice_mood) -- (SA); \draw[arrow] (econ) -- (SA); \draw[arrow] (econ) -- (SB); \draw[arrow] (bob_mood) -- (SB); \draw[arrow] (SA) -- (A); \draw[arrow] (SB) -- (B); % Arrows that skip a level \draw[arrow] (alice_mood) to[bend right] (A); \draw[arrow] (bob_mood) to[bend left] (B); \end{tikzpicture} $
Вершины соответствуют событиям / случайным величинам, ребра ведут из непосредственной причины в непосредственное следствие. Значение величины в каждой вершине - функция от значений в её предках и случайного шума, причем шумы в разных вершинах независимы.
(не уверен, что добавление вершин с настроением на что-то влияет, но пусть для наглядности будет)
События $X$ и $Y$ независимы при любом условии, выразимом чере $Z$ ($Z$ - набор вершин), если:
1) для любой цепи (пути $X \to Q_1 \to \ldots \to Q_n \to Y$), $Z$ содержит хотя бы одну вершину из цепи
2) для любой вилки (пути $X \leftarrow Q_1 \leftarrow Q_2 \leftarrow \ldots \leftarrow Q_N \to P_1 \to \ldots \to P_M \to Y$), $Z$ содержит середину вилки $Q_N$
3) для любой обратной вилки ($X \to Q_1 \to Q_2 \to \ldots \to Q_N \leftarrow P_1 \leftarrow \ldots \leftarrow P_M \leftarrow Y$), $Z$ не содержит вершин, достижимых из середины вилки $Q_N$ (в том числе саму $Q_N$).

[lel0lel]

mihaild в сообщении #1702511 писал(а):

вот из Вашего равенства уже не следует, например, $P((A, B) | (S_A, \neg S_B)) = P(A | S_A) P(B | \neg S_B)$ - а, наверное, хотелось бы.

А можете это пояснить. На первый взгляд так и будет, если на принятие решения ехать или не ехать полное влияние оказывает получение собственной премии. Другими словами $P(A| (S_A, \neg S_B, \text{иные совместные условия})) = P(A | S_A)$

[mihaild]

lel0lel в сообщении #1702551 писал(а):

На первый взгляд так и будет, если на принятие решения ехать или не ехать полное влияние оказывает получение собственной премии

Да, этого хочется. Но из равенства $(1)$ это не следует. Поэтому равенство $(1)$ не является хорошей формализацией.

[lel0lel]

А если так:
$P(A|B S_A S_B) = P(A |S_A)=P(A B S_A S_B)/P(B S_A S_B)$, то $P(A B S_A S_B)=P(A |S_A)P(B S_A S_B);$
$P(B|S_A S_B)=P(B|S_B)=P(B S_A S_B)/P(S_A S_B)$, то $P(B S_A S_B)=P(B|S_B)P(S_A S_B)$.
Тогда $P(A B S_A S_B)=P(A |S_A)P(B|S_B)P(S_A S_B)$ или $P(A B|S_A S_B)=P(A |S_A)P(B|S_B).$
Это не к вопросу о формализации, а скорее к стартовому вопросу.

[Утундрий]

lel0lel в сообщении #1702557 писал(а):

А если так...

Цитата:

Нечитабельность — это свойство чего-либо (например, текста или рукописи), заключающееся в том, что это невозможно прочесть или очень трудно для чтения. Это может быть связано как с качеством самого написанного текста (например, нечёткие буквы, неразличимый почерк), так и с его содержанием (убогость или непонятность).

[lel0lel]

(Оффтоп)

Ещё нечитаемость бывает от нежелания читать)

[mihaild]

lel0lel
Я тоже не очень понимаю, где предположения, и что доказывается.

[lel0lel]

Виноват, значит действительно нечитаемо набрал. Доказывается формула $P((A,B)|(S_A,S_B))=P(A |S_A)P(B|S_B).$ Используется $P(A| (S_A, S_B, \text{иные совместные условия, но не связанные явно с А})) = P(A | S_A)$, аналогично для $B$, и формула условной вероятности. Завтра попробую добавить комментарии.

[mihaild]

Это понятно: $P(AB | S_A S_B) = P(A | S_A S_B) \cdot P(B |A S_A S_B)$ (всегда), $P(A|S_AS_B) = P(A|S_A)$ (по условию), $P(B|A S_A S_B) = P(B | S_B)$ (если $A$ "не свяазано явно" с $B$).
Но ещё, наверное, хочется $P(A | S_A \overline{S_B}) = P(A | S_A)$. А это отдельное условие.

[lel0lel]

mihaild в сообщении #1702598 писал(а):

Но ещё, наверное, хочется $P(A | S_A \overline{S_B}) = P(A | S_A)$. А это отдельное условие.

Это вроде бы можно доказать, если использовать $P(A|S_AS_B) = P(A|S_A)$. Проверьте:

$$\begin{align}P(A | S_A)=&P(A | S_A(\overline{S_B}+S_B))=\frac{P(A S_A\overline{S_B})+P(A S_AS_B)}{P(S_A)}=\\& \frac{P(A |S_A\overline{S_B})P(S_A\overline{S_B})+P(A| S_AS_B)P(S_AS_B)}{P(S_A)}=\\&P(A |S_A\overline{S_B})P(\overline{S_B}|S_A)+P(A| S_AS_B)P(S_B|S_A)=\\& P(A|S_A\overline{S_B})(1-P(S_B|S_A))+P(A|S_A)P(S_B|S_A). \end{align}$$

Из начала этой выкладки и из конца получаем: $P(A|S_A)(1-P(S_B|S_A))=P(A|S_A\overline{S_B})(1-P(S_B|S_A)).$ Если $S_A, \overline{S_B}$ совместны, то $P(A|S_A\overline{S_B})=P(A|S_A).$

[mihaild]

Да, правда, я тут пожадничал. У нас обе части на подпространстве, где $S_A$ выполнено, так что это обычное утверждение "если $A$ не зависит от $S_B$, то не зависит и от $\neg S_B$".

[lel0lel]

Вообще, не вижу каких-то проблем ввести понятие условно независимых событий. Насколько это полезно -- судить не берусь. Может, действительно, просто лишняя терминология.
Определение:
Будем говорить, что события $A, B$ условно независимые при условии $C$ (это тоже некоторое событие), если $P(AB|C)=P(A|C)P(B|C).$
Очевидно, что два совместных события $A,B$ являются условно независимыми при условии $AB$
Два "истинно" независимых события легко могут оказаться условно зависимыми. Например, $A$ - выпадение $5$ на первом кубике, $B$ - выпадение $5$ на втором независимом кубике $P(AB)=P(A)P(B)=1/36$. Но если наложить условие $C$ -- сумма чисел в двух бросках равна $11$, то условной независимости уже не будет, поскольку $P(AB|C)=0$, но $P(A|C)=P(B|C)=1/2$. Похожая ситуация с экстремумом функций нескольких переменных -- локальный экстремум у функции был, а условного может и нет или наоборот.
В общем, прям захотелось теорию создавать, исследованиями заняться, но потом погуглил и остыл
https://en.wikipedia.org/wiki/Conditional_independence

[mihaild]

lel0lel в сообщении #1702697 писал(а):

Будем говорить, что события $A, B$ условно независимые при условии $C$ (это тоже некоторое событие), если $P(AB|C)=P(A|C)P(B|C).$

mihaild в сообщении #1702511 писал(а):

Введём обозначение: $A \perp\!\!\!\perp B | C$ - "$A$ не зависит от $B$ при условии $C$" - означающий $P(A|BC) = P(A|C)$