Аппроксимация полупростых

[Yadryara]

Размышляя о применимости HL1 к тем или иным задачам, попытался аппроксимировать A036351. Результат получился на удивление хороший, хотя не уверен что сходимость продолжится.

$$1.5589\int\limits_{2}^{x}\frac{dt}{\ln^{\frac34}t}$$

Сравнил вычисления по этой формуле с фактическими количествами полупростых:

x=10^     Относительная
            погрешность
1              3.419593
2              1.023039
3              0.464207
4              0.253071
5              0.154188
6              0.102021
7              0.071561
8              0.051699
9              0.037906
10             0.027978
11             0.020643
12             0.015134
13             0.010954
14             0.007769
15             0.005346
16             0.003519
17             0.002166
18             0.001194
19             0.000531
20             0.000123
21            -0.000074
22            -0.000094
23             0.000033

Почему так получается пока не понимаю.

[vicvolf]

Yadryara
А зачем? Ведь есть известная асимптотическая формула.

[Yadryara]

vicvolf в сообщении #1702122 писал(а):

Ведь есть известная асимптотическая формула.

Значит она не всем известна. Вы, например, её пока не привели.

Интервал   Первонач  Полупрост        2       3        Троек
<=10^3           93         67       39      27           13
<=10^4         1429        732      291     197           71
<=10^5        18257       7321     2170    1505          379
<=10^6       214694      69811    16783   11546         2377
<=10^7      2419224     658013   130805   89606        15197
<=10^8     26538772    6186940  1049769  717517       103474
<=10^9    286024010   58236914  8636829 5885913       741791

А вот из этих 5-ти столбцов какие можно аппроксимировать и как?

Третий столбец — это тоже количество бесквадратных полупростых, только специального вида.
Последний столбец — это количество троек из A039833.

[icosahedron2]

chat gpt писал(а):

For $x \ge 2$ let $S(x)$ denote the count of semiprimes $\le x$ (integers that are the product of two primes, not necessarily distinct). The standard asymptotic formula is

$$S(x) = \frac{x \log \log x}{\log x} + O\left(\frac{x}{\log x}\right)$$

​

[vicvolf]

Вот более точная формула:

$$\pi_2(x)=\int_2^x {\frac{(\ln\ln(t)+2\gamma-1)dt}{\ln(t)}}+O(x/\ln^2(x)),$$

где $\gamma$ - постоянная Эйлера-Маскерони.

[Yadryara]

icosahedron2 в сообщении #1702158 писал(а):

product of two primes, not necessarily distinct)

Как раз обязательно различных простых. Чтобы было именно 4 делителя у таких чисел.

vicvolf, спасибо. Правда, по поводу большей точности не уверен. Сравнил по последней формуле:

1    0.404425
2    0.261666
3    0.134007
4    0.063738
5    0.027141
6    0.008901
7   -0.000419
8   -0.005961
9   -0.009571
10  -0.012030
11  -0.013778
12  -0.015057
13  -0.016018
14  -0.016754
15  -0.017327
16  -0.017778
17  -0.018136
18  -0.018423
19  -0.018653
20  -0.018839
21  -0.018989
22  -0.019109
23  -0.019205

[Yadryara]

Всё-таки что-то здесь не то. vicvolf, Вы эту формулу откуда взяли? Тоже у ИИ спросили и адаптировали?

Я подумал, что может надо взять обычные полупростые A036352 и сравнить с их количествами. Сравнил:

1    -0.297787
2     0.113235
3     0.092288
4     0.053607
5     0.024285
6     0.008094
7    -0.000653
8    -0.006032
9    -0.009592
10   -0.012036
11   -0.013780
12   -0.015058
13   -0.016018

Дальше погрешность уже совпадает с предыдущей табличкой с точностью до миллионных. То есть тоже увеличивается вместо того чтобы стремиться к нулю.

То есть Ваша формула неверна. С чего Вы взяли что она более точная? Вы что не проверяли?

[icosahedron2]

Yadryara в сообщении #1702161 писал(а):

Как раз обязательно различных простых. Чтобы было именно 4 делителя у таких чисел.

Это не важно. Квадратов простых $\pi (\sqrt{x}) = O(\sqrt{x})$, и на асимптотику они не влияют. Вроде у меня получилось вывести асимптотику

$$ S(x) \sim \frac{x \ln \ln x}{\ln x} $$

с помощью ТРПЧ. Каждое полупростое имеет простой делитель $p < \sqrt{x}$. Всего будет $\pi (x / p)$ полупростых кратных $p$. Соответственно $S(x) \sim \sum_{p < \sqrt{x}} \pi (x / p)$. Таким способом будут дважды посчитаны полупростые, у которых оба простых делителя меньше $\sqrt{x}$, но на асимптотику это не влияет.

$$S(x) \sim \sum_{p < \sqrt{x}} \pi (x / p) \sim \sum_{p < \sqrt{x}} \frac{x/p}{\ln (x/p)} \sim \frac{x}{\ln x} \sum_{p < \sqrt{x}} \frac{1}{p(1 - \ln p / \ln x)}$$

Так как

$$\sum_{p < \sqrt{x}} \frac{1}{p(1 - \ln p / \ln x)} \sim \sum_{p < \sqrt{x}} \frac{1}{p} \sim \ln \ln x$$

то формула для $S(x)$ доказана. ​Медленная сходимость, возможно, связана с медленной сходимостью использованных асимптотических формул, в особенности $\sum_{p < \sqrt{x}} \frac{1}{p(1 - \ln p / \ln x)} \sim \ln \ln x$.

[Yadryara]

icosahedron2 в сообщении #1702251 писал(а):

Квадратов простых $\pi (\sqrt{x}) = O(\sqrt{x})$, и на асимптотику они не влияют.

Согласен.

icosahedron2 в сообщении #1702251 писал(а):

Медленная сходимость, возможно, связана с медленной сходимостью использованных асимптотических формул, в особенности $\sum_{p < \sqrt{x}} \frac{1}{p(1 - \ln p / \ln x)} \sim \ln \ln x$.

А как Вы определили что она медленная? Можно взглянуть на сравнение с фактами?

Или Вы имеете в виду что для $x=10^{23}$ надо попросту посчитать
$ \frac{x \ln \ln 10^{23}}{\ln 10^{23}} $ с каким-то кэфом, но Вы не знаете с каким?

[icosahedron2]

Yadryara в сообщении #1702264 писал(а):

А как Вы определили что она медленная? Можно взглянуть на сравнение с фактами?

Я предположил, что раз функция $\ln \ln x$ растёт медленно, то и сходимость медленная. Не исключаю, что это не так.

Хотя есть ещё одна причина медленной сходимости. $\pi(x)$ более точно оценивается интегральным логарифмом. А в доказательстве используется $\pi (x) \sim \frac{x}{\ln x}$, откуда возникает ошибка порядка $\frac{x}{\ln^2 x}$. ​

[Yadryara]

icosahedron2 в сообщении #1702268 писал(а):

$\pi(x)$ более точно оценивается интегральным логарифмом.

Конечно. У меня как раз в формуле интегральный логарифм. Хотя и не в первой степени.

icosahedron2 в сообщении #1702268 писал(а):

Не исключаю, что это не так.

Так а чего же тут исключать или не исключать, когда можно взять и проверить? Эталонные значения известны аж до $10^{23}$.

icosahedron2 в сообщении #1702268 писал(а):

откуда возникает ошибка порядка $\frac{x}{\ln^2 x}$. ​

Для $10^{23}$ отличие гораздо больше. Что делаем?

[vicvolf]

Yadryara в сообщении #1702217 писал(а):

То есть Ваша формула неверна. С чего Вы взяли что она более точная? Вы что не проверяли?

Формула верная.

vicvolf в сообщении #1702159 писал(а):

$$\pi_2(x)=\int_2^x {\frac{(\ln\ln(t)+2\gamma-1)dt}{\ln(t)}}+O(x/\ln^2(x)),$$

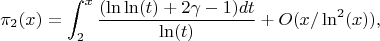
где $\gamma$ - постоянная Эйлера-Маскерони.

Ее точность выше по отношению к формуле (тоже верной)

icosahedron2 в сообщении #1702158 писал(а):

For $x \ge 2$ let $S(x)$ denote the count of semiprimes $\le x$ (integers that are the product of two primes, not necessarily distinct). The standard asymptotic formula is

$$S(x) = \frac{x \log \log x}{\log x} + O\left(\frac{x}{\log x}\right)$$

​

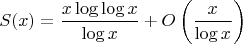
И для этого не надо считать. Сравните формулы остаточных членов. В первой формуле его порядок меньше.

Абсолютная ошибка естественно растет и в первой и во второй формуле, так как растут остаточные члены. А вот относительная ошибка в обеих формулах должна стремиться к нулю, так как формулы асимптотические.
Например, в последней формуле:

$$|\frac{S(x)}{\frac{x\ln\ln(x)}{\ln(x)}}-1|=O(\frac{1}{\ln\ln(x)}),$$

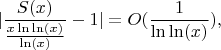
т.е. сходимость очень медленная. Поэтому могут быть нюансы при вычислениях.

-- 18.09.2025, 18:32 --

Yadryara в сообщении #1702126 писал(а):

Последний столбец — это количество троек из A039833.

Вот это интересный случай. Здесь может быть использована модификация гипотезы Харди-Литтлвуда для кортежей из полупростых чисел.

[Yadryara]

vicvolf в сообщении #1702277 писал(а):

И для этого не надо считать.

Надо. Практика — критерий истины.

И она пока даёт худшие результаты по обеим этим формулам.

vicvolf в сообщении #1702277 писал(а):

Абсолютная ошибка естественно растет и в первой и во второй формуле,

А при чём тут абсолютная, если я с самого начала считал только относительную?