Вариант 1:
Вероятность системы находиться в состоянии с энергией

при термодинамическом равновесии пропорциональна
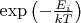
Тогда вероятность найти систему в состоянии с энергией в промежутке
![$[E, E+dE]$ $[E, E+dE]$](https://dxdy-03.korotkov.co.uk/f/2/c/a/2ca6bcc54bc3770e9314d3fe7b1600db82.png)
как будто бы
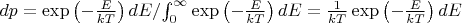
.
Но если так, тогда можно отсюда получить среднюю энергию системы при равновесии:
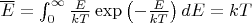
И выходит, будто она для любой системы равна

, но это ведь не так.
Вариант 2: Вероятность найти частицу, находящуюся при термодинамическом равновесии в потенциале U(x), в интервале
![$[x, x+dx]$ $[x, x+dx]$](https://dxdy-01.korotkov.co.uk/f/0/7/6/076b6754a07de7f359cd18d37baebe5482.png)
равна:
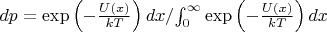
.
Но такая интерпретация не согласуется с использованием закона распределения Больцмана при выводе формулы Планка (см. например, Сивухин, "Оптика"), где предполагается, что вероятность осциллятора найтись в состоянии с энергией
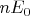
пропорциональна
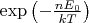
(что совсем никак не связано с пространственным распределением и, скорее, походит на интерпретацию 1).