Доброго времени суток.
Задача: На доске написано

различных натуральных чисел. Известно, что среднее арифметическое любых

или

чисел является целым числом.
а) Могут ли на доске одновременно быть записаны числа
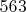
и
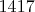
?
После увиденного решения собственное кажется сумбурным. Но я хотел бы проверить свои рассуждения.
Мое решение.
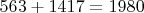
Пронумеруем неизвестные нам числа-

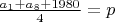
Где

-целое.
Отсюда вывод- все числа должны быть нечётными. Сумма любых двух чисел должна делится на

, а нам уже даны два нечётных числа.
Разность
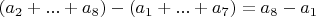
должна делится на

имеем
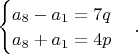
Считаем
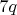
чётным, так как оно разность двух нечётных. перепишем
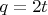
Складывая уравнения системы получим противоречие.
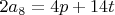
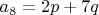
Слева нечётное, справа чётное число.
Итог: Числа
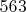
и
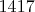
не могут быть записаны одновременно на доске.
Я не знал как подойти к решению и пошёл длинным путем. Интересует проверка решения на предмет ошибок.