Тензорное произведение линейных пространств

[Anton_Peplov]

В учебнике Кострикин. Введение в алгебру. т. 2. Гл. 6. Тензоры $\S 1$. Начала тензорного исчисления п. 5. Тензорное произведение пространств есть определение тензорного произведения линейных пространств, сводящееся к следующему (если я все правильно понял). Сохраняю оригинальные обозначения, но порядок изложения чуть-чуть меняю.

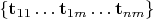
Рассмотрим $n$-мерное линейное пространство $V$ и $m$-мерное линейное пространство $W$, $T$ - $nm$-мерное линейное пространство над одним и тем же полем $\Re$. Зафиксируем в $V$ базис $\{ \mathbf e_1 \dots \mathbf e_n \}$, в $W$ - базис $\{ \mathbf f_1 \dots \mathbf f_m \}$, в $T$ - базис $\{ \mathbf t_{11} \dots \mathbf t_{1m} \dots \mathbf t_{nm} \}$. 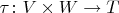определим отображение $\tau \colon V \times W \to T$ так:

$$ \tau \left (\sum_{i=1}^n \alpha_i \mathbf e_i, \sum_{j=1}^m \beta_j \mathbf f_j \right ) = \sum_{i=1}^n \sum_{j=1}^m \alpha_i \beta_j \mathbf t_{ij} \eqno{(LS.prod)} $$

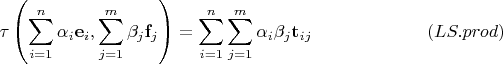
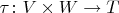
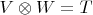
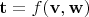
Если построена функция $\tau \colon V \times W \to T$ упомянутого вида, то говорят, что пространство $T$ является тензорным произведением пространства $V$ на пространство $W$ и пишут $V \otimes W = T$. В свою очередь, вектор $\mathbf t = f(\mathbf{v, w})$ называется тензорным произведением вектора $\mathbf v$ на вектор $\mathbf w$, что обозначается $\mathbf{v \otimes w = x}$.

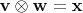
Что меня смущает, так это следующая цитата:

Кострикин писал(а):

$\tau$ - сюръективное отображение, т.е.

$$ T = \langle \tau \mathbf{(v, w) | v} \in V, \mathbf w \in W \rangle_\Re $$

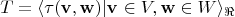
Что меня заставляет думать, что Кострикин неправильно употребил слово "сюръекция".

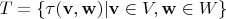
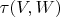
1. В соответствии с общепринятым определением сюръекции, должно было быть написано $T = \{ \tau\mathbf{(v, w) | v} \in V, \mathbf w \in W \}$. Написанная же Кострикиным формула означает, что $T$ - это линейная оболочка множества $\tau(V, W)$. Конечно, формально линейное пространство и есть его же собственная линейная оболочка, но зачем бы было огород городить.

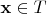
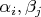
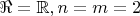
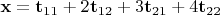
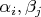
2. Нетрудно продемонстрировать такой вектор $\mathbf x \in T$, чтобы было невозможно подобрать нужные коэффициенты $\alpha_i, \beta_j$ в уравнении (LS.prod). Например, пусть $\Re = \mathbb R, n = m = 2$ и $\mathbf x = \mathbf t_{11} + 2\mathbf t_{12} + 3\mathbf t_{21} + 4\mathbf t_{22}$. Если я вконец не разучился считать, решения (LS.prod) относительно $\alpha_i, \beta_j$ не существует.

3. Вообще говоря, известный факт, имеющий большое значение в квантовой механике, что тензорное произведение линейных пространств состоит не только из тензорных произведений векторов этих пространств.

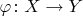
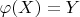
Заглянул в первый том, где Кострикин определяет сюръекцию. Определение сюръекции у него стандартное: функция $\varphi \colon X \to Y$ есть сюръекция, когда $ \varphi (X) = Y$. То ли он ее потом где-то переопределил, то ли просто ошибся с термином.

Вопросы:
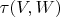
1. Я правильно понимаю, что $T$ не есть $\tau(V, W)$, а есть линейная оболочка $\tau(V, W)$ ?
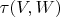
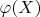
2. Встречался ли кто-нибудь с употреблением термина "сюръекция" в линейной алгебре в том смысле, что $Y$ есть линейная оболочка $\varphi (X)$ ? Или это отдельный глюк в отдельном учебнике?

[Утундрий]

Anton_Peplov в сообщении #1701801 писал(а):

в $T$ - базис

Возникает резонный вопрос, а что это за $T$? Тем более, что про $V$ и про $W$ всё было сказано.

[dgwuqtj]

1. Да.
2. Я такое впервые вижу.

[Anton_Peplov]

Утундрий в сообщении #1701803 писал(а):

Возникает резонный вопрос, а что это за $T$?

Виноват. Забыл написать, что $T$ - $nm$-мерное пространство над тем же полем. Дополню стартовый пост.

dgwuqtj
Спасибо!

[Утундрий]

(О бурбакизмах)

Парадоксально, но решительное продвижение на ниве запоминания этих ваших терминов в моей биографии сыграл Анджей Сапковский, уничижительно упомянувший некий гипотетический "Булонь сюр Мьерд" (перевод нагуглите, пожалуйста, сами). После столь мощной подсказки и в силу осознавания центральной роли би- все три термина "стали мне абсолютно понятны".