Или сразу без разложения подставлять? Но на каком основании?
Какая связь между существованием предела и подстановкой?
Формально, запись, в которой участвует

означает "какая-то функция

, такая, что
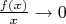
, но какая именно - не скажем".
Разность двух таких функций это снова такая функция, что и означает
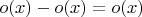
.
И
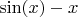
- это тоже такая функция, что и означает
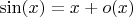
.
Может помочь нумеровать

.
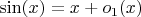
(тут уже

- совершенно конкретная функция). И
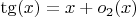
. Обозначив
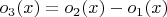
, получаем
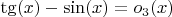
- тут уже никакой асимптотики, это просто равенство функций (но при этом
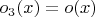
.